Stanを使って変数選択したい
背景
Stanを使ってモデリングをしている時に不満を感じる点として、変数選択が難しいということが挙げられます。もともと私自身は、例えばStepwiseやLassoなどを用いた"機械的な"変数選択があまり好きではない1のですが、それでも分析を効率的に進める上でそれらの手法に頼りたくなることがあります。
そういったときにglmを用いているのであればstep関数により容易に変数選択が可能なのですが、Stanではそうもいきません。何か良い方法はないかと探していたところ、StanのGithubレポジトリに{projpred}というそれっぽいlibraryを見つけたので、紹介がてら変数の選択精度を実験してみます2。
データ準備
ライブラリの読み込み
今回の分析では{rstan}の代わりに{rstanarm}というlibraryを使用します。{rstanarm}はRのglmと同じようなシンタックスのままでモデルをベイズ化することが可能で、例えば{rstanarm}のvignetteでは以下のようなスニペットが紹介されています(一部改変あり)3。
library(rstanarm) data("womensrole", package = "HSAUR3") womensrole$total <- womensrole$agree + womensrole$disagree womensrole_bglm_1 <- stan_glm(cbind(agree, disagree) ~ education + gender, data = womensrole, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4, cores = 1, seed = 123)
> womensrole_bglm_1 stan_glm family: binomial [logit] formula: cbind(agree, disagree) ~ education + gender observations: 42 predictors: 3 ------ Median MAD_SD (Intercept) 2.5 0.2 education -0.3 0.0 genderFemale 0.0 0.1 Sample avg. posterior predictive distribution of y: Median MAD_SD mean_PPD 24.3 0.8 ------ For info on the priors used see help('prior_summary.stanreg').
数字の意味は一旦置いておきますが、今回はこちらのlibraryを使用しながら進めていきます。
続いて他のlibraryを読み込みます。この辺りはvignetteそのままです。
library(projpred) library(ggplot2) library(bayesplot) theme_set(theme_bw()) options(mc.cores = parallel::detectCores())
シミュレーションデータの作成
実験を進めるにあたりシミュレーションデータを作成します。もちろんlibraryに付属のデータセットを使っても良いのですが、そのまま同じことをするのも面白くないので以下のように複数のデータを作成して結果を比較してみましょう:
- 説明変数の数が少なく(20)、連続変数のみ
- 説明変数の数が多く(100)、連続変数のみ
- 説明変数の数が少なく(20)、ダミー変数を含む
- 説明変数の数が多く(100)、ダミー変数を含む
見てわかる通りで、説明変数の数とダミー変数の有無によって4パターンを用意します。なぜこのパターンにしたかというと、単純にvignetteを見ていて連続変数ばかりだなと思ったのと、サンプルデータの説明変数の数が20ぐらいで、これなら機械的な選択に頼らなくても自力でどうにかできそうだな、と思ったためです。
各パターンについて特にひねりもなくデータを作成します。なお真のモデルは1と2、3と4で同一のものとしました。したがって2と4の状況は、1と3それぞれに比べて「不要なデータのみが追加された状態」での変数選択という状況になります。
以下のように各パラメータを設定します。
set.seed(1) N <- 100 # number of observations xn_1 <- 20 # number of variables for pattern 1 xn_2 <- 100 # number of variables for pattern 2 b1 <- 0.5 # regression coefficient of X[, 1] b2 <- 0.8 # regression coefficient of X[, 2] var_e <- 1 # residual variance
パターン1 & 2について、まず乱数によりXを生成し、そのうちの2列を使ってYを作成します。またその2列を含む20列および全列を各パターンの説明変数とします。
X <- matrix(rnorm(N * xn_2, 0, 1), nrow = N, ncol = xn_2) Y <- 1.0 + X[, 1] * b1 + X[, 2] * b2 + rnorm(N, 0, var_e) X1 <- X[, 1:xn_1] X2 <- X[, 1:xn_2] dat1 <- data.frame("Y" = Y, "X" = I(X1)) dat2 <- data.frame("Y" = Y, "X" = I(X2))
データセットを作成する際にX1をI()で渡すことで、X1全体を"X"として再定義できます。すると以下のようなformulaが実行可能になります。
> lm(Y ~ X, dat1) Call: lm(formula = Y ~ X, data = dat1) Coefficients: (Intercept) X1 X2 X3 X4 X5 X6 1.038393 0.422365 0.824111 0.006940 -0.064897 0.060024 -0.004623 X7 X8 X9 X10 X11 X12 X13 -0.096471 0.040521 0.123807 -0.051311 0.125116 0.009435 0.014924 X14 X15 X16 X17 X18 X19 X20 0.065920 -0.037135 -0.110772 -0.015537 -0.003969 -0.136834 0.095512
もちろんそのまま渡して.で指定するのでも構いません。
tmp <- data.frame("Y" = Y, "X" = X1)
> lm(Y ~ ., tmp) Call: lm(formula = Y ~ ., data = tmp) Coefficients: (Intercept) X.1 X.2 X.3 X.4 X.5 X.6 1.038393 0.422365 0.824111 0.006940 -0.064897 0.060024 -0.004623 X.7 X.8 X.9 X.10 X.11 X.12 X.13 -0.096471 0.040521 0.123807 -0.051311 0.125116 0.009435 0.014924 X.14 X.15 X.16 X.17 X.18 X.19 X.20 0.065920 -0.037135 -0.110772 -0.015537 -0.003969 -0.136834 0.095512
続いてパターン3 & 4についても基本的に同じ流れでデータを作成しますが、一部にダミー変数を含めます。
Z <- matrix(rnorm(N * xn_2, 0, 1), nrow = N, ncol = xn_2) Z[, seq(1, 100, 10)] <- if_else(Z[, seq(1, 100, 10)] > 0, 1, 0) Y <- 1.0 + Z[, 1] * b1 + Z[, 2] * b2 + rnorm(N, 0, var_e) X3 <- Z[, 1:xn_1] X4 <- Z[, 1:xn_2] dat3 <- data.frame("Y" = Y, "X" = I(X3)) dat4 <- data.frame("Y" = Y, "X" = I(X4))
フィッティング
stan_glmによるフィッティング
では、これらのデータを用いてフィッティングをしてみましょう。スクリプトは以下のようになります:
n <- N D <- xn_1 p0 <- 5 # prior guess for the number of relevant variables # scale for tau (notice that stan_glm will automatically scale this by sigma) tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) # regularized horseshoe prior fit1 <- stan_glm(Y ~ X, family = gaussian(), data = dat1, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_2 p0 <- 5 tau0 <- p0/(D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit2 <- stan_glm(Y ~ X, family = gaussian(), data = dat2, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_1 p0 <- 5 tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit3 <- stan_glm(Y ~ X, family = gaussian(), data = dat3, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_2 p0 <- 5 tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit4 <- stan_glm(Y ~ X, family = gaussian(), data = dat4, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
実行画面は省略します。
結果の確認
無事にフィッティングが終わったのでまずは結果を確認しましょう。fit1オブジェクトには多くの情報が格納されていますが、以下のようにパラメータの分布を確認します(結果は一部抜粋)。
> fit1$stan_summary mean se_mean sd 2.5% 10% 25% 50% 75% 90% 97.5% n_eff Rhat (Intercept) 1.026278e+00 0.0012818960 0.08107422 0.87096060 0.92283578 9.695387e-01 1.025776e+00 1.083455e+00 1.12962235 1.18570039 4000.000 1.0002199 X1 3.908290e-01 0.0016254360 0.09798225 0.19341915 0.26638997 3.278100e-01 3.940279e-01 4.542220e-01 0.51236797 0.57793402 3633.750 0.9999048 X2 8.240328e-01 0.0013608445 0.08516982 0.65884688 0.71552972 7.672683e-01 8.238806e-01 8.816342e-01 0.93310548 0.98857084 3917.008 0.9995082 X3 -1.059357e-03 0.0005388889 0.03408233 -0.08025937 -0.03484370 -1.106505e-02 -1.177711e-04 1.032889e-02 0.03180827 0.07368474 4000.000 1.0005552 X4 -1.872770e-02 0.0007089570 0.04483838 -0.13979248 -0.07768171 -3.228712e-02 -3.977780e-03 3.213492e-03 0.01638515 0.04656703 4000.000 0.9998376 X5 2.138502e-02 0.0006738661 0.04261903 -0.03511247 -0.01201396 -1.858049e-03 6.263328e-03 3.500771e-02 0.07857940 0.13847975 4000.000 0.9993905# ︙ # 以下省略 # ︙
この結果を見るとX1とX2で概ね設定通りの値が得られているようですね。
ではここから{projpred}による変数選択に取り掛かりましょう。スクリプトは以下のようになります:
sel1 <- varsel(fit1, method = 'forward')
> sel1$varsel$vind # variables ordered as they enter during the search X2 X1 X20 X16 X19 X11 X5 X14 X18 X4 X7 X9 X8 X17 X10 X15 X13 X12 X3 X6 2 1 20 16 19 11 5 14 18 4 7 9 8 17 10 15 13 12 3 6
おおっ!ちゃんと1列目と2列目が選ばれていますね!下記のプロットを見ても、3番目以降の変数はモデルの精度に対して寄与していないことがわかると思います。なおここでelpdはexpected log predictive densityを指しますが、ちょっと情報量規準辺りの話はうかつに解説できないのでvignetteを引用するに留めておきます。
The loo method for stanreg objects provides an interface to the loo package for approximate leaveone-out cross-validation (LOO). The LOO Information Criterion (LOOIC) has the same purpose as the Akaike Information Criterion (AIC) that is used by frequentists. Both are intended to estimate the expected log predictive density (ELPD) for a new dataset.
varsel_plot(sel1, stats=c('elpd', 'rmse'))

各パラメータの分布についても見てみましょう。上位5個に選ばれた説明変数に限定してプロットしてみます。
# Visualise the three most relevant variables in the full model mcmc_areas(as.matrix(sel1), pars = names(sel1$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2))

効果のなかった変数は0を中心に集中して分布していることがわかります。
残りの各パターンについても同様に見ていきますが、個別に確認するのは面倒なので一度にまとめてしまします。
sel2 <- varsel(fit2, method = 'forward') sel3 <- varsel(fit3, method = 'forward') sel4 <- varsel(fit4, method = 'forward')
> sel2$varsel$vind X2 X1 X87 X24 X83 X71 X89 X18 X95 X85 X4 X67 X19 X16 X60 X56 X55 X53 X42 X20 2 1 87 24 83 71 89 18 95 85 4 67 19 16 60 56 55 53 42 20 > sel3$varsel$vind X2 X14 X4 X1 X18 X5 X16 X3 X9 X15 X19 X20 X6 X8 X17 X11 X7 X12 X13 X10 2 14 4 1 18 5 16 3 9 15 19 20 6 8 17 11 7 12 13 10 > sel4$varsel$vind X2 X90 X74 X45 X64 X14 X25 X52 X60 X4 X20 X16 X22 X1 X63 X41 X9 X26 X53 X5 2 90 74 45 64 14 25 52 60 4 20 16 22 1 63 41 9 26 53 5
むむ。。。
いずれのパターンでも2列目はちゃんと選ばれていますが、パターン3と4では1列目が選ばれていませんね。 プロットも見てみましょう。
varsel_plot(sel2, stats=c('elpd', 'rmse')) varsel_plot(sel3, stats=c('elpd', 'rmse')) varsel_plot(sel4, stats=c('elpd', 'rmse'))

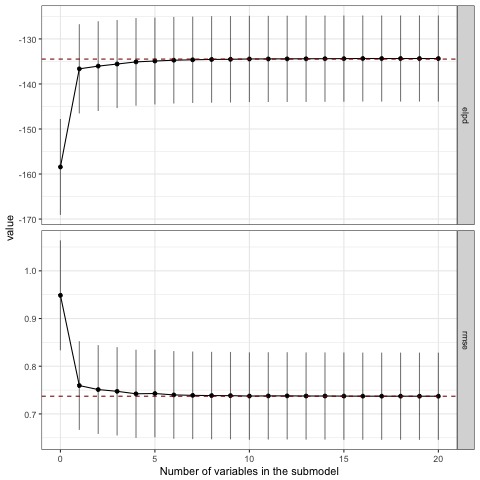
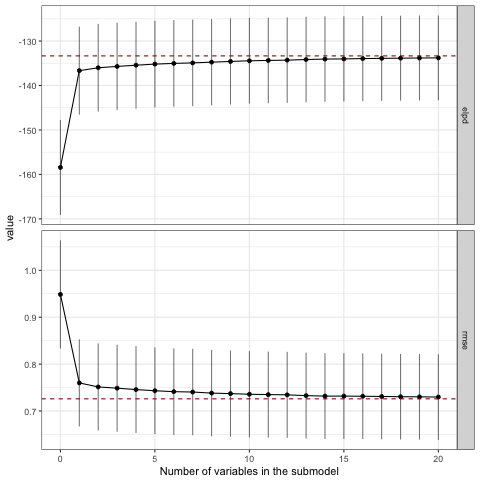
正しい変数セットが選ばれていないので当然ですが、2変数目ですでにフルモデルにおけるelpdやrmseと接するようになっており、モデルの精度改善に貢献しているのは1変数目だけという結果になっています。
パラメータの分布を見ても、パターン1と比較するといずれも分布の裾が広くなっています。さらにパターン3では正の効果を受けたためか右に裾を引く形とはなっているものの、効果のない他の変数とほとんど変わらない分布となってしまいました。ダミー変数はパラメータの推定が難しいようです。
mcmc_areas(as.matrix(sel2), pars = names(sel2$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2)) mcmc_areas(as.matrix(sel3), pars = names(sel3$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2)) mcmc_areas(as.matrix(sel4), pars = names(sel4$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2))



追試
では、ダミー変数が含まれる場合に真のパラメータを捉えることができる確率としてはどの程度になるのでしょうか。パターン3を100回繰り返し、そのうち何回真の変数セットを選択できるか確認してみましょう。
n <- 100 t <- 100 D <- 20 p0 <- 5 b1 <- 0.5 b2 <- 0.8 tau0 <- p0 / (D-p0) * 1/sqrt(n) out <- matrix(0, t, 2) for (i in 1:t) { x <- matrix(rnorm(n * D, 0, 1), nrow = n) x[, seq(1, D, 5)] <- ifelse(x[, seq(1, D, 5)] > 0, 1, 0) y <- 1.5 + x[, 1] * b1 + x[, 2] * b2 + rnorm(n, 0, 1) dat <- data.frame("y" = y, "x" = I(x)) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit0 <- stan_glm(y ~ x, family = gaussian(), data = dat, prior = prior_coeff, chains = 4, iter = 2000) sel0 <- varsel(fit0) out[i, ] <- names(sel0$varsel$vind[1:2]) }
> table(out[, 1]) x2 100 > table(out[, 2]) x1 x10 x11 x12 x13 x14 x15 x17 x18 x19 x20 x3 x4 x5 x6 x7 x9 55 2 2 3 3 1 1 5 5 1 1 2 7 4 1 4 3
なんと、連続変数である2列目の選択確率は100%である一方、ダミー変数である1列目は約半数しか選択されないという結果になりました。もちろん回帰係数の大小にも影響されるのでしょうが、結構衝撃的な結果に思えます。
終わりに
これまでの実験の結果をまとめると以下のようになりそうです:
- 連続変数であれば説明変数を20から100に増やしても大きな問題なく変数を選択できそう
- ダミー変数の変数選択は難しく、今回の条件の場合、半分の確率で失敗する
- ダミー変数はパラメータの推定も難しい
実際のデータ分析の現場では真のパラメータを予め知ることができないため、変数選択の結果を受け入れざるを得ないことがあるかと思います。しかし今回の実験の結果からは「真の変数セットを選択できる確率は半分程度しかない」ことが示されており、機械的な変数の取捨選択がどれほど危険であるかを教えてくれているのではないでしょうか。
とは言え今回実験に使用した{projpred}は便利なlibraryであると思いますので、これから活用しつつも引き続き変数選択の方法について探していこうと思います。