Ad-Stock効果を推定しつつ回帰を回したい⑤
背景
しつこいようですが、Marketing Mix Modeling(MMM)の話題です。
先日、こんな面白い論文を見つけました。 GoogleのResearcherによるMMMの論文(彼らはMedia Mix Modelingと呼んでいます)なのですが、ヒルの式を用いて広告のShape効果(Carveture効果)を推定するということをやっています。ここでShape効果・carveture効果とは、メディアの露出量に対する目的変数の反応を示す曲線を指すようで、ヒルの式とは:
$$ H(x; K, S) = \frac{1}{1 + (\frac{x}{K})^{-S}} $$
であり、$K > 0$や$S > 0$となるパラメータによってLogやSigmoidの形状を表現することができるようです。
ヒルの式によってxがどのような形状となるか、実際に確認してみましょう。まずはヒルの式を以下のように定義します。
hill_transformation <- function(x, k, s) { 1 / (1 + (x / k)^-s) }
続いて、パラメータとなるkとsをそれぞれ以下のように設定した場合をプロットしてみましょう。なおこの数値は論文から拝借しています。
x <- seq(0, 1, by = 0.05) plot(x, hill_transformation(x, 0.4, 4), type = "l", col = 2, xlim = c(0, 1), ylim = c(0, 1), ylab = "Hill Transformed Value") par(new = T) plot(x, hill_transformation(x, 0.4, 1), type = "l", col = 3, xlim = c(0, 1), ylim = c(0, 1), axes = F, ylab = "") par(new = T) plot(x, hill_transformation(x, 0.8, 4), type = "l", col = 4, xlim = c(0, 1), ylim = c(0, 1), axes = F, ylab = "") par(new = T) plot(x, hill_transformation(x, 0.8, 1), type = "l", col = 5, xlim = c(0, 1), ylim = c(0, 1), axes = F, ylab = "") legend("topleft", legend = c("k = 0.4, s = 4", "k = 0.4, s = 1", "k = 0.8, s = 4", "k = 0.8, s = 1"), col = c(2:5), lty = rep(1, 4))
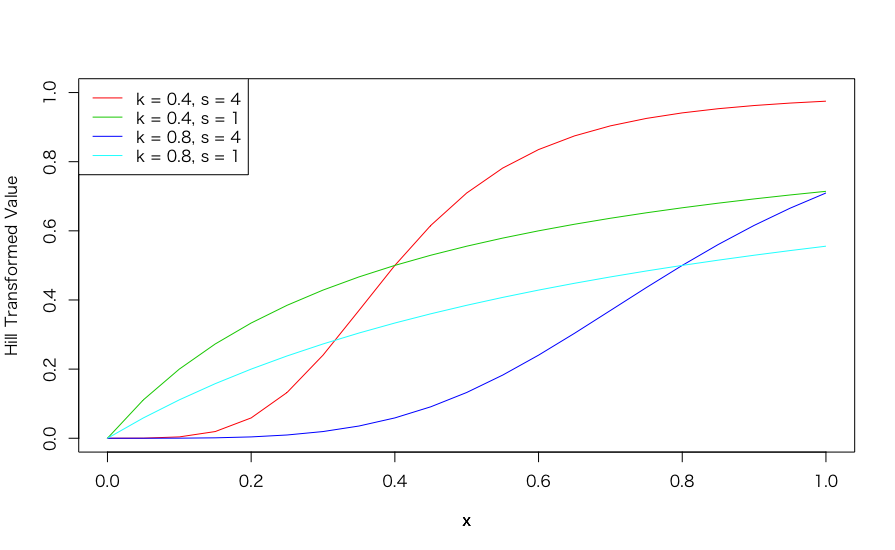
このように、パラメータを変更することで元の値を柔軟に変換することが可能です。これまで私が書いてきた記事では、いずれも広告効果(回帰係数)そのものを推定する方法にばかり注目しており、説明変数の"効き方"については触れてきませんでした。これではちょっと検討が足りないと言われても仕方ありません。
というわけで本エントリーでは、ヒルの式により変換したXを用いてシミュレーションデータを発生させ、元のXから変数変換のためのパラメータを推定できるかを検証したいと思います。なお元論文ではAd-Stock効果としてGeometric Ad-Stock:
$$ GA(x_{t}; \alpha, L) = \frac{\sum_{l = 0}^{L}x_{t-l}\alpha^{l}}{\sum_{l = 0}^{L}\alpha^{l}} $$
を用いていますが、今回の検証ではAd-Stock効果をみておらず、説明変数の生の値を変換しています1。
ライブラリの読み込み
今回の分析でも{rstan}を使用します。
library(tidyverse) library(ggplot2) library(rstan) options(mc.cores = parallel::detectCores()) rstan_options(auto_write = TRUE)
シミュレーションデータの生成
分析用のデータ生成ですが、まず説明変数X1をrunifにより作成します。次に与えたパラメータからヒルの式を用いて変換し、目的変数yを作成します。
## データ生成用の関数を定義 simulate_y <- function(pars) { n <- pars[1] # num of observation mu <- pars[2] # intercept var_e <- pars[3] # residual variance beta_01 <- pars[4] # regression coefficient of X1 to be esitmated # lambda_01 <- pars[5] # decay rate of Ad-Stock effect of X1 k_01 <- pars[6] # k for X1 s_01 <- pars[7] # s for X1 X_01_raw <- runif(n) X_01_conv <- hill_transformation(X_01_raw, k_01, s_01) error <- rnorm(n, 0, sqrt(var_e)) y <- mu + beta_01 * X_01_conv + error dat <- data.frame( "Y" = y, "X_01" = X_01_raw, "X_01_conv" = X_01_conv ) return(na.omit(dat)) } ## データ生成 set.seed(123) pars <- c(100, 5, 0.1, 0.8, 0.7, 0.4, 4) dat <- simulate_y(pars)
X1について、
- 推定したい広告効果 ⇒
0.8 - ヒルの式の
kおよびs⇒0.4および4
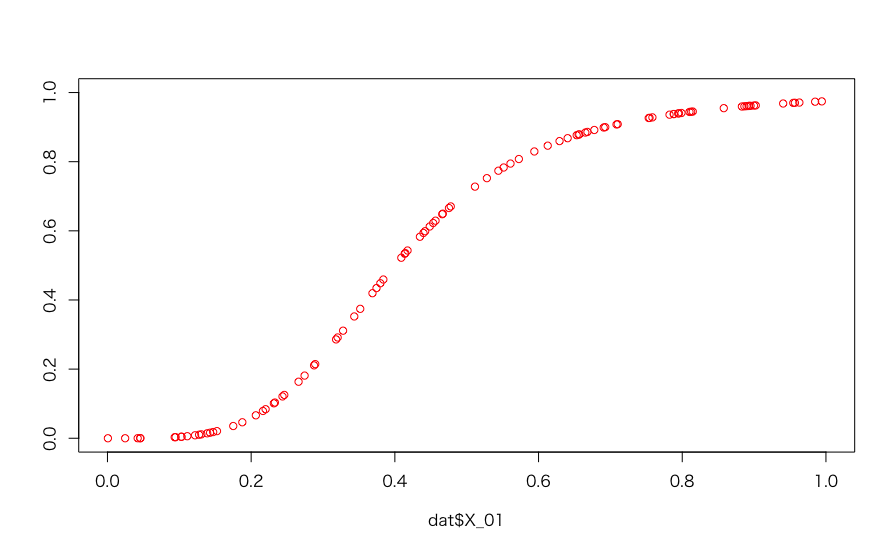
と指定しており、これらのパラメータを元のX_01から推定することが狙いです。ちなみに今回のパラメータではX_01と変換後のX_01は以下のようになります:
plot(dat$X_01, dat$X_01_conv, col = 2, xlim = c(0, 1), ylim = c(0, 1), ylab = "")
optimによるフィッティング
手始めにoptimを使ってフィッティングしてみましょう。これまでの記事でも度々optimを使ってきましたが、なかなか精度良く推定することが可能です。ただしAICを計算するのが面倒なのでここではbetaを直接推定しないことにして、lmを使います。よって推定対象はk_01とs_01の2つだけです。
return_AIC <- function(param, dat) { k_01 <- param[1] s_01 <- param[2] dat$X_01_conv <- hill_transformation(dat$X_01, k_01, s_01) AIC(lm(Y ~ X_01_conv, dat)) }
### 適当な数値を入れてみる > return_AIC(rep(0.5, 2), dat) [1] 60.47417
ちゃんと動くようなのでフィッティングしてみましょう。
param <- rep(1, 2) res_optim <- optim(par = optim(par = param, fn = return_AIC, dat = dat)$par, fn = return_AIC, dat = dat)
パラメータを確認してみると:
true_par <- c(0.8, 0.4, 4) dat$X_01_conv_opt <- hill_transformation(dat$X_01, res_optim$par[1], res_optim$par[2]) optim_par <- c(coef(lm(Y ~ X_01_conv_opt, dat))[2], res_optim$par)
> print(cbind(true_par, optim_par), digits = 2) true_par optim_par X_01_conv_opt 0.8 1.1 0.4 0.5 4.0 1.9
うーん、sがちょっと外れているようですね。推定された値でのプロットを見てみましょう。
plot(dat$X_01, hill_transformation(dat$X_01, 0.4, 4), col = 2, xlim = c(0, 1), ylim = c(0, 1), ylab = "Hill Transformed Value") par(new = T) plot(dat$X_01, hill_transformation(dat$X_01, res_optim$par[1], res_optim$par[2]), col = 3, xlim = c(0, 1), ylim = c(0, 1), axes = F, ylab = "") legend("topleft", legend = c("k = 0.4, s = 4", "k = 0.49, s = 1.9"), col = c(2:3), lty = rep(1, 2))
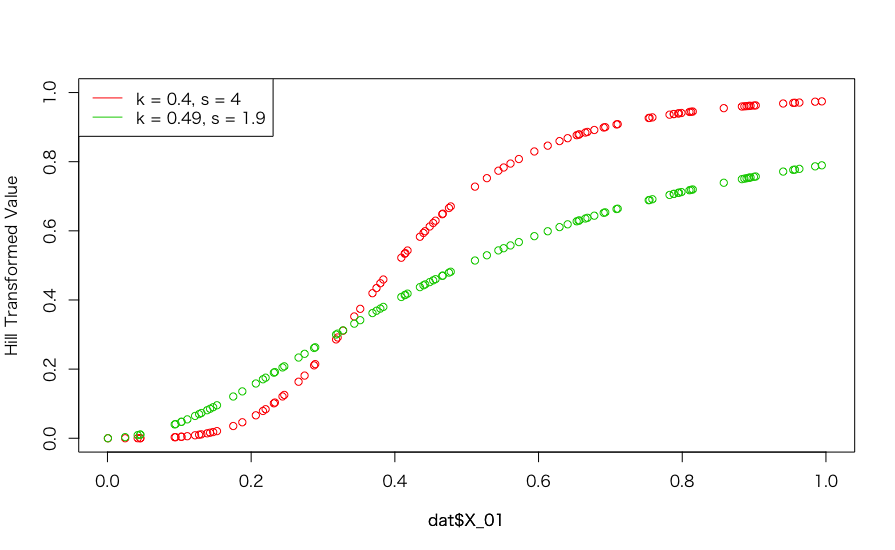
ちょっとカーブのメリハリがなく、全体として直線的になってしまっています。これが今回のサンプルで偶々発生したものなのか、それともsの推定に何らかの偏りがあるのか確かめてみましょう。同様の試行を1,000回繰り返してみます。
## 5番目のパラメータはAd-Stockのλだが今回は不使用 pars <- c(100, 5, 0.1, 0.8, 0.7, 0.4, 4) n <- 1000 res_optim_all <- matrix(NA, n, 3) param <- rep(1, 2) try_s <- function(pars) { dat <- simulate_y(pars) res_optim <- optim(par = optim(par = param, fn = return_AIC, dat = dat)$par, fn = return_AIC, dat = dat) dat$X_01_conv_opt <- hill_transformation(dat$X_01, res_optim$par[1], res_optim$par[2]) return(c(coef(lm(Y ~ X_01_conv_opt, dat))[2], res_optim$par)) } for (i in 1:n) { res_optim_all[i, ] <- tryCatch(try_s(pars), error = function(e) return(rep(0, 3))) }
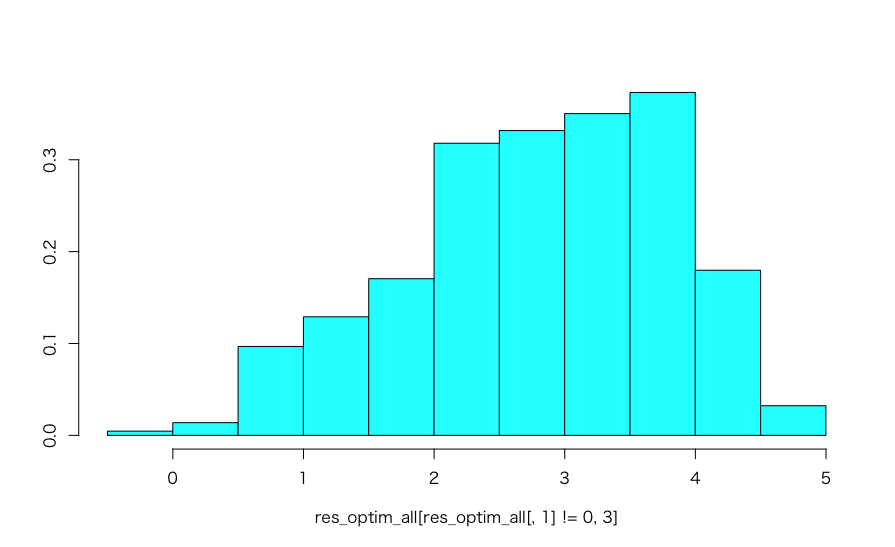
tryCatchを使って無理やりループを回しましたが、やはり推定が不安定なようで全体の4割ちょっとしか収束していません。その収束した解のバラツキを見てみても以下のようにかなり広がってしまっており、真値である4も中心とはなっていませんね。
> nrow(res_optim_all[res_optim_all[, 1] != 0.0, ]) [1] 434
MASS::truehist(res_optim_all[res_optim_all[, 1] != 0, 3])
Stanによるフィッティング
では今度はStanを使ってみましょう。以下のように指定します。
### データの再作成 set.seed(123) pars <- c(100, 5, 0.1, 0.8, 0.7, 0.4, 4) dat <- simulate_y(pars) dat_Stan <- list(N = nrow(dat), Y = dat$Y, X_01 = dat$X_01 )
またStanのスクリプトは以下のようになります。今回は特別な指定はしていませんが、X_01_convを作成するためにtransformed_parametersブロックを置いています。
data { int N; vector[N] Y; vector[N] X_01; } parameters { real mu; real beta_01; real<lower=0, upper=1> shape_k_01; real<lower=0, upper=5> shape_s_01; real<lower=0> var_error; } transformed parameters { vector[N] X_01_conv; for(k in 1:N) { X_01_conv[k] = 1 / (1 + (X_01[k] / shape_k_01)^-shape_s_01); } } model { // Sampling for(i in 1:N) { Y[i] ~ normal(mu + beta_01 * X_01_conv[i], var_error); } }
上記のモデルを用いて、フィッティングしてみましょう。
fit_01 <- stan(file = '/YourDirectory/Hill_Transformation.stan', data = dat_Stan, iter = 10000, chains = 4, seed = 123)
結果の確認
フィッティングが終わったので、結果を見てみましょう。fit_01からサンプルを抽出して加工します。
## サンプルを抽出する res_01 <- rstan::extract(fit_01) ## 該当するパラメータを取り出す ests <- summary(fit_01)$summary beta_rows <- rownames(ests)[grep("beta", rownames(ests))] shape_rows <- rownames(ests)[grep("shape", rownames(ests))]
まずは収束の判断です。Rhatが1.1未満であることを確認した上で、トレースプロットとヒストグラムを見てみましょう。
stan_trace(fit_01, pars = beta_rows) stan_trace(fit_01, pars = shape_rows) stan_hist(fit_01, pars = beta_rows) stan_hist(fit_01, pars = shape_rows)



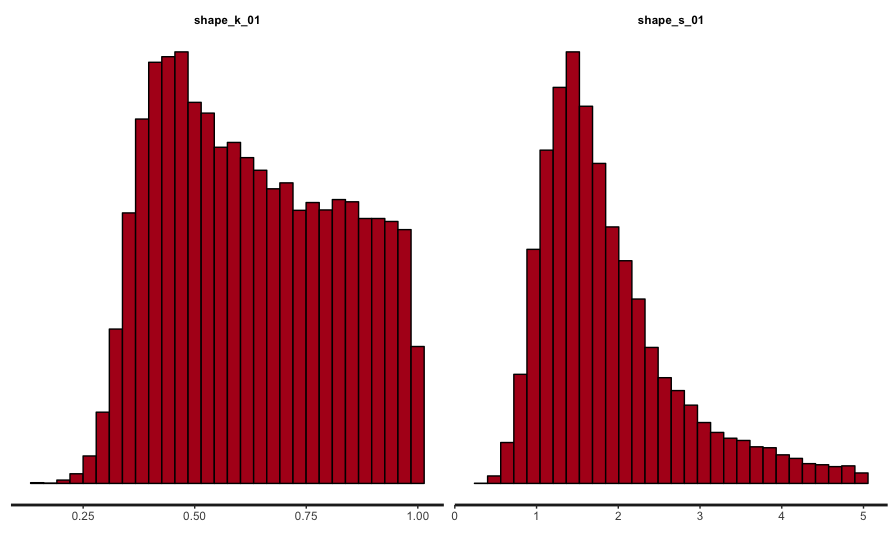
うーん、kが全体的に広がっていたり、sは真値とかけ離れたところにピークがあったり、推定に失敗している様子ですね。
ひとまず回帰係数の推定結果を見てみましょう。実際の値と推定値を並べてみます。
beta_par <- ests %>% data.frame %>% select(mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% beta_rows)
> sprintf("True = 0.8, Stan_Est = %.3f, Optim_Est = %.3f", beta_par$mean, optim_par[1]) [1] "True = 0.8, Stan_Est = 1.369, Optim_Est = 1.111"
あらら、optimの結果よりも外れてしまいました。Shape効果の方はどうでしょうか。
> ests %>% + data.frame() %>% + select(mean) %>% + mutate(Par = rownames(ests), + Type = "Stan") %>% + filter(Par %in% shape_rows) %>% + bind_rows(data.frame( + mean = c(0.4, 4, optim_par[-1]), + Par = rep(c("shape_k_01", "shape_s_01"), 2), + Type = c(rep("True", 2), rep("Optim", 2)) + )) %>% + spread(Type, mean) %>% + select(Par, True, Stan, Optim) Par True Stan Optim 1 shape_k_01 0.4 0.6308075 0.4965623 2 shape_s_01 4.0 1.8736434 1.9041772
こちらもoptimの方がまだ設定値に近いようですね。ただoptimもstanもどちらもうまく推定できていない様子なので比較に意味はないかもしれませんが。
終わりに
というわけで、今回はあまりパッとしない結果となってしまいました。元論文はちゃんと読んでいないのですが、彼らは階層ベイズで解いているようなので、もう少しパラメータに対して制約をかけてあげないとダメなのかもしれません。
本当なら良い推定値が得られるようになるまで頑張りたいのですが、ひとまず思いつくことは試した上でこの結果なので、いったん諦めて公開することとしました。何かアイディアが浮かべば再挑戦したいと思います。
-
要するにAd-Stock効果のパラメータの同時推定がうまく行かなかったんです。。。↩