集団の繁栄に必要な子どもの数について考える
※今回の内容はDr.STONEという漫画のネタバレを含みます
唐突ですが、Dr.STONEという漫画が好きです。
物理や化学に詳しくないので内容を理解しながら読めているわけではないのですが、石化した世界で少しずつ文明のレベルが上がっていくのを見ていると、科学って地道だけど面白いなーと思ってしまいます。
しかし読んでいて一点気になるところがありました。 白夜たちが宇宙から地球に帰還した後、3組のカップルから石神村が誕生したことです。
もちろんそれぞれのカップルが非常にたくさんの子どもを産めば可能でしょう。しかし現代人が10人も20人も子どもを産めるのかというと少し難しいような気もします。 またカップルが3組しかありませんので、子どもが少なければあっと言う間に「全員が親戚同士」みたいなこととなり、新たなカップルを作れなくなりそうな気もします。そう考えると実際にどれだけ厳しい条件だったんだろうかと気になってしまいました。
というわけで今回は白夜たちが将来的に集団を繁栄させるために、どの程度の子どもをもうける必要があったかを考えてみたいと思います。
考え方
上記を考えるにあたり、以下のような条件でシミュレーションを実施します:
- スタートは男性3人女性3人とする(第一世代)
- 各世代において男女1人ずつでカップルとなる
- 男女の数が異なる場合、余った人は子どもを残さない
- 各カップルはそれぞれ
np人の子どもを産む npは世代をまたぐ全てのカップルで共通とする- 生まれてくる子どもの性別は男女比 1:1 でランダムに決まる
- カップルは一夫一妻制を取り、パートナー以外の異性との子どもは産まない
- 世代をまたがってカップルを形成しない
シミュレーションしやすいよう厳しめの条件としています。ただしこのままでは近縁者とのカップルが出来てしまいますので、以下の条件を追加します:
- 子どもの近交係数が一定の値以上となるカップルは形成しない
ここで近交係数とは集団遺伝学などで使われる用語で、近親交配の程度を表します。日本ではいとこ同士での結婚が法律上認められていますが、いとこ同士の子どもの近交係数が6.25%となります。第一世代の数が少ないため、ここを厳しくするとあっと言う間にカップルが出来なくなることが予想されます。
上記のシミュレーションを実行するためのプログラムは以下としました:
generate_population <- function(np, # カップルが産む子どもの数 n0 = 6, # 第一世代の人数 num_column = 6, # 結果格納用のテーブルの列数 G = 5, # シミュレートする世代数 random_seed = 42, # 乱数固定用 rel_lim = 0.90 # 血縁係数(近交係数とは異なる) ) { set.seed(random_seed) # 子ども性別を決めるのに乱数を使うため pairs <- c() # カップルを記録する用のテーブル ### 個人ごとの記録(ID、世代、性別、近交係数、父、母)を格納するテーブル res_mat <- matrix(0, n0, num_column) colnames(res_mat) <- c("ID", "Gen", "Sex", "Inbred", "Father", "Mother") ### 第一世代の生成 res_mat[, "ID"] <- 1:n0 res_mat[, "Gen"] <- 1 res_mat[, "Sex"] <- rep(c(1, 0), 3) ### 以下、将来世代を生成 for(g in 1:G) { ### 現在世代の血縁関係を評価する rel_mat <- create_rel_mat(res_mat) ### カップルを作るペアを決める tmp_pairs <- make_pairs(g, res_mat, rel_mat, rel_lim) pairs <- rbind(pairs, tmp_pairs) ### np人の子どもを生成する tmp_res_mat <- generate_progenies(tmp_pairs, res_mat, g, np, num_column) ### それぞれの近交係数を計算する(近交係数は両親間の血縁係数*1/2) tmp_res_mat <- calculate_inbred_coef(tmp_res_mat, rel_mat) res_mat <- rbind(res_mat, tmp_res_mat) # sprintf("The %d generation generated", g+1) print(g) } return(res_mat) }
お試し
さて、関数の解説は後回しにしてまずは実行してみましょう。このプログラムを実行すると以下のような結果が得られます。
source("/YourDirectory/my_functions.r") # 関数を定義したファイル res_mat <- generate_population(np = 3, G = 15)
> calc_num_pop(res_mat) Gen Population 1 1 6 2 2 9 3 3 6 4 4 9 5 5 9 6 6 12 7 7 15 8 8 18 9 9 24 10 10 33 11 11 30 12 12 39 13 13 54 14 14 60 15 15 60 16 16 87
plot(calc_num_pop(res_mat), type = "l", xlab = "Generation g", ylab = "Population size")
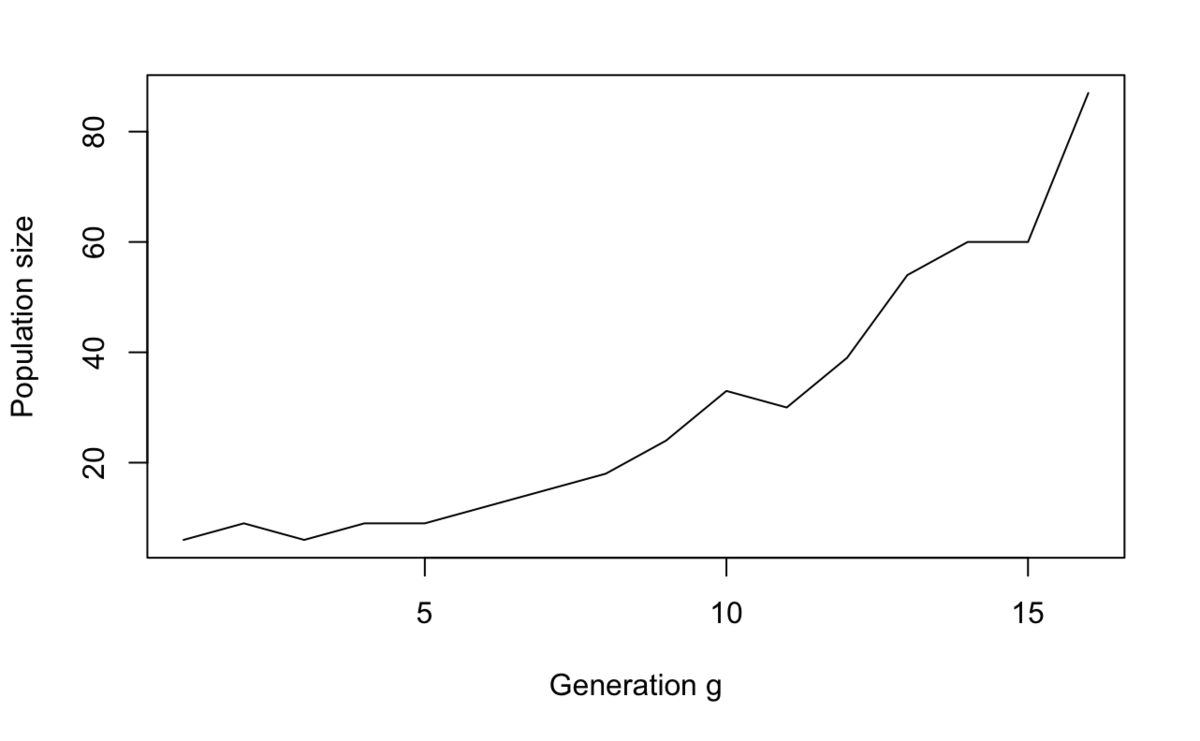
この表とグラフは先の条件でシミュレーションを実施したときの世代ごとの人数を集計しています。
第五世代まではなかなか人数が増えていきませんが、第六世代から徐々に人数を増やせていますね。カップルごとの子どもの数が3人というのは少し多いようにも思えますが、昭和24年ごろの第一次ベビーブームの合計特殊出生率が4.32ということらしいので*1、あり得ない数値ではないでしょう。むしろ死亡を一切考慮していないシミュレーションなので、もっと産んでいないと3人でも怪しくなりそうです。とはいえ、これなら石神村も問題なく誕生するでしょう、めでたしめでたし…
…と、言いたいところですが、結論づける前に近交係数を見てみましょう。
> summary(res_mat[, "Inbred"]) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.0000 0.2956 0.3209 0.3051 0.3377 0.4053
なんと近交係数が平均で30%、最大で40%にもなってしまっています。近交係数25%は親子間でのカップルというレベルなので、これは困ってしまいます。
シミュレーション
というわけでここからが本題です。シミュレーションでパラメータとして渡している rel_lim を変更することで、近交が高まるのを避けながら集団を繁栄させ、無事に石神村を誕生させることができるか見てみましょう。
まずは日本の法律で認められているいとこ同士まで許容する(近交係数6.25%、すなわち両親間の血縁係数12.5%のカップルまで認める)とどうなるでしょうか。
> res_mat <- generate_population(np = 3, G = 15, rel_lim = 0.125) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
なんと、途中でカップルを作ることができなくなってしまいます…。もしかして seed によるのかもしれませんので、いくつか試してみましょう。
> generate_population(np = 3, G = 15, rel_lim = 0.125, random_seed = 1) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
> generate_population(np = 3, G = 15, rel_lim = 0.125, random_seed = 2) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
> generate_population(np = 3, G = 15, rel_lim = 0.125, random_seed = 3) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
ダメなようです…。
ちなみにですが、近交の制限をなくしても(同世代内のどんな近縁者とのカップルも認めても)男女の偏りによって集団が存続しないこともあります。例えば以下のように、 rel_lim を1としても seed によっては途中で止まってしまいます。
> res_mat <- generate_population(np = 3, G = 15, rel_lim = 1.0, random_seed = 5) [1] 1 [1] 2 [1] 3 [1] 4 [1] 5 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
白夜たちはもともと厳しい条件に置かれていたことがわかりますね。
それでは逆に、近交係数の条件を保った場合に必要となる np を考えてみましょう。4人から順番に増やしてみます:
> res_mat <- generate_population(np = 4, G =15, rel_lim = 0.125) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
〜〜 以下省略 〜〜
> res_mat <- generate_population(np = 8, G =15, rel_lim = 0.125) [1] 1 [1] 2 [1] 3 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
9人まで増やすと計算がなかなか終わらなかったため打ち切ってしまいましたが、この条件(日本の法律に合わせたカップル)はかなり厳しいようです。そもそも子どもを9人産むというのも結構難しそうですしね。
近交係数の条件をもう少し緩め、12.5%まで認めることにしてみましょう。ちなみにこの12.5%というのはおじ・姪、おば・甥でのカップルに相当します。
> res_mat <- generate_population(np = 4, G = 15, rel_lim = 0.250) [1] 1 [1] 2 [1] 3 [1] 4 [1] 5 make_pairs(g, res_mat, rel_mat, rel_lim) でエラー: Couldn't make any couple!
4人ではダメ。5人では?
> res_mat <- generate_population(np = 5, G = 15, rel_lim = 0.25) [1] 1 [1] 2 [1] 3 [1] 4 [1] 5 [1] 6 [1] 7
今度は計算が終わりませんでした…。一晩待ったのですが…。
しかし第八世代まで進むことは確認したので、これなら可能性がありそうです。つまり、
ことで石神村を無事に誕生させることができそうです。やったね白夜! *2
このときの近交係数がどうなっているかも確認しておきましょう。
### 第七世代までで止める res_mat <- generate_population(np = 5, G = 7, rel_lim = 0.25)
> calc_inb(res_mat) Gen Inbred_Coef 1 1 0.0000000 2 2 0.0000000 3 3 0.0000000 4 4 0.0625000 5 5 0.0937500 6 6 0.1132812 7 7 0.1250000 8 8 0.1191406
近交係数の平均は第七世代で12.5%と上限に達していますが、第八世代ではわずかに減少しています。
> calc_num_pop(res_mat) Gen Population 1 1 6 2 2 15 3 3 25 4 4 50 5 5 115 6 6 245 7 7 505 8 8 1195
また、世代ごとの人数を見ると第八世代で大幅に増えているので、これ以降は近交を高めることのないカップルを安定して作れることが期待できます。
もう少しプログラムをうまくかければこの辺りを追えるかもしれないのですが、実装力の無さが恨めしい…。
終わりに
というわけで、地球に降り立った6人を始祖として集団を繁栄させることが本当にできるのかを検証してみたわけですが、結果としては「厳しい条件ながらも不可能ではなさそう」ということが見えてきました。
次回はこの検証に用いた関数の具体的な解説をしたいと思います。
*1:https://www8.cao.go.jp/shoushi/shoushika/meeting/taikou_4th/k_1/pdf/ref1.pdf
*2:漫画では白夜以外のメンバーが割とすぐに亡くなっている様子なので、実際には5人というのも難しいでしょうけど
glmnetをもう少し理解したい⑤
それでは前回の記事に続いてelnet1の紹介です。前回の記事はこちらです。
ループ③(回帰係数の推定)
以上までで見てきた通り、ループ①・②では almすなわちlambdaを更新しつつ、alpha(alf)やpenalty.factor(vp)との乗算によって罰則を計算していました。
ループ③ではその罰則を用いて回帰係数を更新します。
なのでこのループがglmnetにおいてメインとなる処理と言って良いと思います。
ループ③はniに対するループです。ここでniは説明変数の数ですね。k をインデックスとして各説明変数をさらっていきます。
まずjuですが、これは各説明変数列における数値のバラつきの有無を示す 1/0 のベクトルでした。バラつきがない、すなわち全ての数値が同じであれば(ju(k) == 0 )ループ③をスキップします(gotoの向かう先が10371で、ループの範囲も同じく10371となっています)。
do 10371 k=1,ni if(ju(k).eq.0) goto 10371
次にaから k 番目の変数の値をakに格納します。前回記事で追いかけた通り、このa(またはao)が最終的には回帰係数として返ります。
前処理においてa = 0.0で初期化されているのでループの 1 周目時点ではakも 0 ですが、ループ①の 2 周目以降は縮小された回帰係数が入っています。
ak=a(k) ! k 番目の変数の a の値を ak に代入。
続いてuとvを計算します。これらは前回の記事で少し紹介した通り、次のブロックで回帰係数aを更新するためのものです。
uはg(k)にak*xv(k)を加算して計算します。ここでg(k)はstanderdにおいてg(j)=dot_product(y,x(:,j))、つまりyとxの内積として定義されたものでした(yとxはそれぞれ標準化されています)。もしも罰則が付いていなければこの共分散が OLS による回帰係数となるはずです(標準化されているのでxの標準偏差は 1)。
このgにxvで重みをつけたakを加算します。ここでxvは weight を乗じたxの二乗和です。しかしループの 1 周目ではak=0であるためgがそのまま利用されることになります。
このようにして定義されたuの絶対値から罰則を減じたものがvとなります。
u=g(k)+ak*xv(k) v=abs(u)-vp(k)*ab
そしてさらにvが 0 よりも大きい場合(OLS による回帰係数が罰則よりも大きい場合)、
- 「
cl(2,k)」と「sign(v,u)/(xv(k)+vp(k)*dem)」を比較して小さい方を選ぶ - それを「
cl(1,k)」と比較して大きい方を選ぶ
という処理を行い、新たにaとして格納します。
ここでclはglmnet.rでcl = rbind(lower.limits, upper.limits) として定義されたものなので、推定された値を上限と下限の間に抑えようとしていることがわかります。またvが 0 以下の場合は 0 となります。
! a(k) を更新 a(k)=0.0 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem)))
以上が回帰係数の更新を行う処理になります。 ややアッサリしていますが、ここの処理は glmnet を理解する上で極めて重要なのでもう少し説明します。
まず前提として、(Elastic Net ではなく)Lasso では軟閾値作用素と呼ばれる写像を用いて解を推定しています。
ここで軟閾値作用素とは、定数 および
において
の絶対値が
よりも大きければ
を、そうでなければ 0 を返す作用素です:
すなわち、推定された回帰係数(の絶対値)が罰則よりも小さければ 0 に丸めてしまい、大きくても罰則の分だけ係数を縮小してしまう、ということです。 一般に Lasso は効果の小さな変数の回帰係数を 0 に縮小する方法として知られていますが、実装としてはこのような軟閾値作用素が用いられており、これを見ると「Lasso はスパースな解を推定できる」という言葉の意味がわかるのではないでしょうか。推定したら 0 になるわけではなく、明示的に 0 にしているのだと。
ここで少し余談なのですが、Lasso や Ridge に関する参考書などを読んでいると「幾何学的な説明」として以下のようなグラフが描かれることがよくあると思います:

このグラフを見るたびに私は納得いかない気分になっていました。と言うのも、Lasso の方(グラフ左側)に着目すると、OLS による推定値の座標(グラフ中の×印の位置)や楕円の広がり方によっては菱形の頂点ではなく辺に接することが普通にあり得そうだからです。 少なくともこのグラフをもって「Lasso は菱形の頂点に接しやすい(ゆえに解が 0 と推定されやすい)」というのは全く自明ではないし直感的でもないな、と思っていました。
そんな時に「機械学習の数理100問シリーズ」の「スパース推定100問 with R」を読んでいると、またも上記のようなグラフが出てきたので悶々としたのですが、次のページには以下のようなグラフがありました:

まさにこれです。このグラフにおいて白色の部分に OLS の推定値がある場合、頂点ではなく辺に接することになります。そこから少しずれて緑色の部分に OLS の推定値が存在する場合には菱形の頂点に接することとなる、つまりいずれか重要でない方の解が 0 として推定されるようになります。
上のグラフのような「幾何学的な説明」は本当に多くの本・記事で見かけるのですが、下のグラフも合わせて説明することでより理解が深まるのでは、と思いました。 余談おわり。
さて、上記のブロックでは、回帰係数が罰則よりも大きく、かつ上限・下限の範囲内であればsign(v,u)/(xv(k)+vp(k)*dem)を新たなaとするのでした。
さきほどの軟閾値作用素の説明においては「罰則を減じた回帰係数」(つまりv)をLasso推定値としていましたが、ここではそれをxv(k)+vp(k)*demで除しています。
これは、ここで得ようとしている推定値というのが Lasso ではなく Elastic Net であるためであり、(第一回で紹介した)教科書(P36)では Elastic Net の推定量を
としています。demはalm*(1-bta)で定義されていたことを思い出すと、これは Ridge (L2)に対する罰則であり、上記の式では $\lambda_{2}$ に該当します。
またxvは X の二乗和を分散で除して 1 を加算したもので、これが何を意味しているのかは以前紹介したときもわからなかったのですが、サンプルデータを使って計算してみるとおおよそ 1 になりそうなのできっとそういう数値なんだろうと思います(適当)。
残る処理ですが、上記によってa(k)が更新されなければループを抜けて次の変数に移ります(gotoの移動先10371はループ③の終点でした)。
またmmが 0 でなければ10391(ループ④の先)に移動するため、以降の処理から次に紹介するループ④までをスキップするようです。
なおこのmmはループ①の1回目では 0 なので1回目は確実に処理が行われるようですね。
またnxは非ゼロとする変数の数の上限なので、推定したパラメータ数がそれを越えると3番目のループを抜けるようです。
if(a(k).eq.ak) goto 10371 if(mm(k) .ne. 0) goto 10391 nin=nin+1 if(nin.gt.nx)goto 10372
ループ④(分散共分散行列の計算)
続いてループ④です。
ここでもループの対象は説明変数(ni)ですが、今度はインデックスとしてjを用い、分散共分散行列(のようなもの)を計算してcに格納するようです。
ここでcはni*nxのサイズの行列です。
このループは短いのでまとめて見てしまいましょう。
まずはjuで変数にバラツキがあるかを確認し、なければ次の変数にスキップします。
続いてmmをチェックし、mmが 0 でなければcにmmを代入して次の変数にスキップします(なおこのmmには後続の処理でninが代入されるのですが、そのninはmmを基準に数値が加算されるような変数となっており互いに入り組んでいて何をやっているのかよくわかりませんでした)。
続いてjとkを比較して同一(同じ変数)だったらcにxvを、同一でなければxのjとkの内積をcに代入します。xvは先ほど出てきたxの二乗和ですので、このcは分散共分散行列のようなものを計算しているようです(正方行列ではないので分散共分散行列とは言わないでしょうけども)。
do 10401 j=1,ni ! バラツキがなければ以降の処理をスキップ if(ju(j).eq.0)goto 10401 ! mm が 0(パラメータが 0 でない)でなければ次のブロックを実行して次の変数へスキップ if(mm(j) .eq. 0)goto 10421 c(j,nin)=c(k,mm(j)) goto 10401 10421 continue if(j .ne. k)goto 10441 ! 変数が同一でなければ 10441 に飛ぶ c(j,nin)=xv(j) ! 同一だったらここ goto 10401 10441 continue c(j,nin)=dot_product(x(:,j),x(:,k)) ! 同一でなかったら j と k の内積をとる 10401 continue ! 4番目のループはここまで
ループ④が終わった後は少しだけ処理が入ります。
mmにはninが代入されます。またiaにはkが入りますが、このkはループ③のインデックスで、ループ③は更新がなければループ④をスキップしてしまうため、パラメータに更新があった変数のインデックスを表すことになります。
その上で、推定された回帰係数の差分を評価し、残差平方和を更新します。
このときg(k)は縮小前の回帰係数(yとx(k)の内積)で、そこから weight調整済みの x の二乗和 を減じたものを残差平方和から減じて計算しています。
continue ! mm に nin を入れる mm(k)=nin ! ia に k を格納 ia(nin)=k 10391 continue ! a(k) の差分をとる。 a(k)、 ak は推定された回帰係数。 del=a(k)-ak ! 残差平方和を更新する rsq=rsq+del*(2.0*g(k)-del*xv(k)) dlx=max(xv(k)*del**2,dlx)
ループ⑤(回帰係数の更新)
さらに続けてループ⑤です。ここは一瞬で終わり、いま計算されたdelを用いてg(j)つまり縮小前の回帰係数を更新します。ところでkはループ③のインデックスで、このループの中では固定されていますので、各変数の回帰係数の縮小に別の変数との共分散を利用しているわけですね。
共分散が大きいということは互いの変数間に相関があるということであり、相関が正なら回帰係数が小さくなるように働くようです。
! 探索範囲は三度説明変数 do 10451 j=1,ni ! インデックスは再度 j を使う if(ju(j).ne.0) g(j)=g(j)-c(j,mm(k))*del 10451 continue ! 5番目のループはここまで continue
ループ⑤を抜けるとすぐにループ③も終了です。
10371 continue ! 3番目のループはここまで
続いて以下のブロックで終了処理の判定を行います。10352まで飛ぶと、いくつか処理はあるもののそのままreturnとなります。つまりdlxがthrよりも小さい、またはninがnxよりも大きい場合にはelnet1を抜けます。
そうではない場合、もう少し処理が続きます。
10372 continue if(dlx.lt.thr)goto 10352 if(nin.gt.nx)goto 10352 if(nlp .le. maxit)goto 10471 jerr=-m return 10471 continue 10360 continue iz=1 da(1:nin)=a(ia(1:nin)) continue 10481 continue nlp=nlp+1 dlx=0.0
ループ⑥(回帰係数の推定・再)
さらに続いてループ⑥です。実はこのループ、以下の通りループ③と処理がほとんど同じです。
! 3番目のループ(一部省略) do 10371 k=1,ni if(ju(k).eq.0)goto 10371 ak=a(k) u=g(k)+ak*xv(k) v=abs(u)-vp(k)*ab a(k)=0.0 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem))) if(a(k).eq.ak)goto 10371 if(mm(k) .ne. 0)goto 10391 nin=nin+1 if(nin.gt.nx)goto 10372 continue mm(k)=nin ia(nin)=k 10391 continue del=a(k)-ak rsq=rsq+del*(2.0*g(k)-del*xv(k)) dlx=max(xv(k)*del**2,dlx) do 10451 j=1,ni if(ju(j).ne.0) g(j)=g(j)-c(j,mm(k))*del ! 6番目のループ do 10491 l=1,nin k=ia(l) ak=a(k) u=g(k)+ak*xv(k) v=abs(u)-vp(k)*ab a(k)=0.0 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem))) if(a(k).eq.ak)goto 10491 del=a(k)-ak rsq=rsq+del*(2.0*g(k)-del*xv(k)) dlx=max(xv(k)*del**2,dlx) do 10501 j=1,nin g(ia(j))=g(ia(j))-c(ia(j),mm(k))*del
ループの対象がniではなくninになっている点が異なりますが、処理としては大体同じなので説明は省略します。
do 10491 l=1,nin k=ia(l) ! k を取り出す( ia には 0 ではないパラメータが推定された変数の列が格納されてる) ak=a(k) ! a を取り出す u=g(k)+ak*xv(k) v=abs(u)-vp(k)*ab a(k)=0.0 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem))) if(a(k).eq.ak)goto 10491 del=a(k)-ak rsq=rsq+del*(2.0*g(k)-del*xv(k)) dlx=max(xv(k)*del**2,dlx)
ループ⑦(回帰係数の更新・再)
ループ⑦も同様にループ⑤と同じ処理をninに対して行っています。
do 10501 j=1,nin g(ia(j))=g(ia(j))-c(ia(j),mm(k))*del 10501 continue ! 7番目のループはここまで
そしてループ⑥が終了。
continue 10491 continue ! 6番目のループはここまで
ここで終了判定が行われます。
nlpはループのカウンターとなっているようで、一定回数を過ぎていなければ10481まで戻されます。
この10481はループ⑥の手前ですので、dlxが十分に小さくなければ再度ループ⑥を実行するような流れになっているようですね。
continue if(dlx.lt.thr)goto 10482 if(nlp .le. maxit)goto 10521 jerr=-m return 10521 continue goto 10481 ! ループ⑥の手前まで戻す 10482 continue da(1:nin)=a(ia(1:nin))-da(1:nin)
ループ⑧(回帰係数の更新・再々)
ループ⑧です。改めて、ninではなくniに対して回帰係数の更新が行われます。
ここでdaにはすぐ上のブロックでaの値からdaの値を減じて更新しているのですが、もう少し上の方でdaにはaを渡しています。
つまり順番としては、da <- a とした上でaを更新し、更新後のaとda(つまり更新前のa)の差分を改めてdaとする、という流れです。
この更新後のdaと分散共分散行列の内積を回帰係数から減じるわけですので、やっていることはループ⑤における回帰係数の更新と同じですね。
do 10531 j=1,ni if(mm(j).ne.0)goto 10531 if(ju(j).ne.0) g(j)=g(j)-dot_product(da(1:nin),c(j,1:nin)) 10531 continue ! 8番目のループはここまで
ループ⑧を抜けると後は終了まで一直線です…と言いたいところですが、ここでなんと衝撃的なことに、10351、つまりループ③の開始まで戻されてしまいます。なんてこった。
実はループ③の開始直後にはiz*jzで処理を変える判定があり、ともに 1 であればループ③の終了時点まで移動するのですが、ここでjzを 0 にしてしまっているので愚直にループ③を再度実行することになります。
しかもjzが 1 に更新される機会があるのはループ③よりも前の段階なので、一度この処理に入った場合には必ずループ③の処理から再開しないといけない、ということですね。
continue jz=0 goto 10351 ! えっ!!
上のgotoを無事に回避できた場合、最後の処理に入ります。
以下では必要な変数を格納しています。
10352 continue if(nin .le. nx)goto 10551 ! nin が nx を超えた場合はここにくる jerr=-10000-m goto 10282 ! jerr を 更新して elnet1 を抜ける 10551 continue if(nin.gt.0) ao(1:nin,m)=a(ia(1:nin)) kin(m)=nin ! m 回目のループの nin を kin[m] に格納する rsqo(m)=rsq ! m 回目のループの rsq を rsqo[m] に格納する almo(m)=alm ! m 回目のループの alm を almo[m] に格納する lmu=m if(m.lt.mnl)goto 10281 if(flmin.ge.1.0)goto 10281 me=0
ループ⑨(回帰係数が推定された変数のカウント)
以下ではelnet1のここまでのループによって推定された回帰係数を確認し、0.0 ではない変数の数をカウントしています。改めて、jは変数、mはlambdaのインデックスです。
! 9番目のループ do 10561 j=1,nin if(ao(j,m).ne.0.0) me=me+1 10561 continue ! 9番目のループここまで
最後にme、rsq、rsq0の確認をし、問題なければ次のlambdaに移ります。
continue if(me.gt.ne)goto 10282 if(rsq-rsq0.lt.sml*rsq)goto 10282 if(rsq.gt.rsqmax)goto 10282 10281 continue ! 1番目のループはここまで 10282 continue deallocate(a,mm,c,da) return end
終わりに
以上でelnet1は終了です。
ここまで随分とかかりましたが、なんとか{glmnet}のメインの処理を最後まで追いかけることが出来ました(途中でわからない部分を飛ばしたりしましたが)。
今回の調査での一番のポイントはやはり、「Lassoでは推定された回帰係数が罰則よりも小さければ 0 に丸めてしまう」ということを確認できたことだと思います。 「Lassoは不要な変数を0として推定することで変数選択できる」というのは間違ってはいないのですが、0として推定できるというよりも明示的に0にしてしまっているという表現の方が正しいと思います。 なので「変数選択できる」という言葉も本来であれば「効果の小さな変数を無視することで変数選択している」という言い方になるのかなと思いました。
こういったモデルにおける重要なポイントを、ソースコードを追いかけながら理解するというのは本当に大事なことだと改めて思います。
それでは。
glmnetをもう少し理解したい④
それでは前回の記事に続いてelnet1の紹介です。過去の記事はこちらです。
ushi-goroshi.hatenablog.com ushi-goroshi.hatenablog.com ushi-goroshi.hatenablog.com
elnet1の実装
前回の記事で最後に触れた通り、elnet1自体は 180 行程度とそれほど大きくはないサブルーチンなのですが、多数のループが込み入っています。
具体的には以下の通り 9 つのループ処理(fortran なので do 文)がネストした構造となっており、 しかもgotoによって行き来しています(わかりやすいように R で書いてありますが、添字は統一してあります)。
# 1番目 for (m in 1:nlam) { # 2番目のループ for (j in 1:ni) { } # 3番目のループ for (k in 1:ni) { # 4番目のループ for (j in 1:ni) { } # 5番目のループ for (j in 1:ni) { } } # 6番目のループ for (l in 1:nin) { # 7番目のループ for (j in 1:nin) { } } # 8番目のループ for (j in 1:ni) { } # 9番目のループ for (j in 1:nin) { } }
前処理
まずはいつもの通り変数の定義ですが、それに加えて初期パラメータを取得するという処理が入ります。
subroutine elnet1(beta,ni,ju,vp,cl,g,no,ne,nx,x,nlam,flmin,ulam,th *r,maxit,xv, lmu,ao,ia,kin,rsqo,almo,nlp,jerr) implicit double precision(a-h,o-z) double precision vp(ni),g(ni),x(no,ni),ulam(nlam),ao(nx,nlam) double precision rsqo(nlam),almo(nlam),xv(ni) double precision cl(2,ni) integer ju(ni),ia(nx),kin(nlam) double precision, dimension (:), allocatable :: a,da integer, dimension (:), allocatable :: mm double precision, dimension (:,:), allocatable :: c allocate(c(1:ni,1:nx),stat=jerr) if(jerr.ne.0) return; ! 初期パラメータを取得 call get_int_parms(sml,eps,big,mnlam,rsqmax,pmin,exmx,itrace) ! a, mm, da を allocate allocate(a(1:ni),stat=jerr) ! a は説明変数の数の次元をもつベクトル if(jerr.ne.0) return allocate(mm(1:ni),stat=jerr) ! mm は説明変数の数の次元をもつベクトル if(jerr.ne.0) return allocate(da(1:ni),stat=jerr) if(jerr.ne.0) return
ここでget_int_parmsはそれほど大きくないので全体を見てみましょう。
以下のようなサブルーチンです:
subroutine get_int_parms(sml,eps,big,mnlam,rsqmax,pmin,exmx,itrace) implicit double precision(a-h,o-z) data sml0,eps0,big0,mnlam0,rsqmax0,pmin0,exmx0,itrace0 /1.0d-5,1.0d-6,9.9d35,5,0.999,1.0d-9,250.0,0/ sml=sml0 eps=eps0 big=big0 mnlam=mnlam0 rsqmax=rsqmax0 pmin=pmin0 exmx=exmx0 itrace=itrace0 return entry chg_fract_dev(arg) sml0=arg return entry chg_dev_max(arg) rsqmax0=arg return entry chg_min_flmin(arg) eps0=arg return entry chg_big(arg) big0=arg return entry chg_min_lambdas(irg) mnlam0=irg return entry chg_min_null_prob(arg) pmin0=arg return entry chg_max_exp(arg) exmx0=arg return entry chg_itrace(irg) itrace0=irg return end
上から3行目のdata文は変数に初期値を与える fortran の記法のようで、dataに続いて宣言した変数に対して/で挟んだ値を初期値として与えるようです。
そのためsml0には 1.0d-5 が、eps0には 1.0d-6 が入力されます。
ここで d は倍精度の指数表記を表します。13行目のentry以降は各変数について特定の値を指定するためのもののようです(entryの使い方がよくわからない…)。
続けていくつか変数に値を代入します。
まずはbtaですが、代入しているbetaは元々parmとして渡されたもので、これはelnet.rでparm = alphaとして渡していたものでした。さらにこのalphaはglmnet.rで定義されたもので、L1 と L2 それぞれに対する罰則の配分を決めるパラメータです:
(なぜか Tex が表示されないのでひとまず)
(1 − \alpha)/2 ||\beta||^2_2 + \alpha||\beta||_1
bta=beta
このbtaを 1 から減じたものをombとしますが、このombはすぐ下で定義されるalmとの乗算でdemを定義する(つまりdem = alm * obm)ためだけに使われています。
さらにalmはループの中で更新されながら最終的にはbtaとの乗算によってabとなり、回帰係数の縮小に使われることになります。
またその次のalfはalmの更新に使われますので、これらの変数がループの中で更新されつつ回帰係数の縮小に利用されるということになります(他にもあります)。
omb=1.0-bta alm=0.0 alf=1.0
以下のブロックではeqsとalfを定義しますが、flminが 1.0以上であればスキップされるようです。
このflminというのはglmnet.rにおいて罰則lambdaが指定されていれば 1
が、されていない時にはlambda.min.ratioが入力される変数でした。
lambda.min.ratioはデフォルトではlambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04)となっていますので 1 よりは小さい値が入りそうです。
したがって以下のブロックは「lambdaが指定されていないときはalfを定義しよう」という処理になっています(eqsはここしか出てきません)。
その場合、epsとflmin(=1)の大きい方を新たにeqsと定義しますが、このeps はget_int_parmsでeps0(1.0d-6 という小さい数)を受け取っていました。
一方lambda.min.ratioは先ほど述べたようにデフォルトではlambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04)となっていますので、もう少し大きい値となりそうです。
したがってeqsは 0.01 or 1e-04 、alfはその1/(nlam-1)乗となるようです。
if(flmin .ge. 1.0)goto 10271 eqs=max(eps,flmin) alf=eqs**(1.0/(nlam-1)) ! alf を eqs の (1/(nlam-1)) で定義する
flminが 1 以上である(lambdaが指定されている)場合は上記をスキップしてこちらにきます。rsqはそのまま残差平方和ですね。
続くaはelnet1の中で重要な役割を担っているのでじっくりと見ていきましょう。
実はこのaは(縮小された)回帰係数を格納する変数です。
10271 continue ! パラメータの初期化 rsq=0.0 ! 残差平方和 a=0.0
このaがどうなるのか、フライングして先の処理を見てみましょう。
elnet1の 70 行目前後に以下の処理があります:
ak=a(k) u=g(k)+ak*xv(k) v=abs(u)-vp(k)*ab a(k)=0.0 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem))) if(a(k).eq.ak)goto 10371
akという変数にaの k 番目の値を渡しておき、uとvを定義し、aの k 番目の値を 0 に更新した上で色んな値を参照しながら再度更新しています(このuやvは後で確認します)。
最終的にaは以下のようにaoという変数に代入されます(154 行目):
if(nin.gt.0) ao(1:nin,m)=a(ia(1:nin))
このaoですが、elnetuの中でelnet1を呼び出すときにはcaという引数として渡されています。
! elnet1 で受け取る変数 ! lmu の次に ao がある subroutine elnet1(beta,ni,ju,vp,cl,g,no,ne,nx,x,nlam,flmin,ulam,th *r,maxit,xv, lmu,ao,ia,kin,rsqo,almo,nlp,jerr) ! elnetu で elnet1 を call するときの引数 ! こちらは lmu の次に ca がある call elnet1(parm,ni,ju,vp,cl,g,no,ne,nx,x,nlam,flmin,vlam,thr,maxi,xv, lmu,ca,ia,nin,rsq,alm,nlp,jerr)
このcaはelnet.rの中で.Fortran("elnet", ...)と call される際に定義される変数でした:
else .Fortran("elnet", ka, parm = alpha, nobs, nvars, as.double(x), y, weights, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, maxit, lmu = integer(1), a0 = double(nlam), # ここで ca が定義されている ca = double(nx * nlam), ia = integer(nx), nin = integer(nlam), rsq = double(nlam), alm = double(nlam), nlp = integer(1), jerr = integer(1), PACKAGE = "glmnet")
ここでnxは説明変数の数、nlamは罰則lambdaの数なので、説明変数の数 × lambda の数のベクトルを定義しています(そしてそれがelnet1の中でaoとして評価・格納される)。
このcaはelnet.rの後続の処理において以下の箇所で抽出されます:
outlist = getcoef(fit, nvars, nx, vnames)
ここでglmnet:::getcoefは以下の通りで、fitとして返ってきたオブジェクトのcaそのものをbetaに格納しています(ninmaxが 0 の場合は 0 のベクトルが返る)。
# glmnet:::getcoef function (fit, nvars, nx, vnames) { # ここまで省略 nin = fit$nin[seq(lmu)] ninmax = max(nin) # ここまで省略 if (ninmax > 0) { # ここで ca を抽出している ca = matrix(fit$ca[seq(nx * lmu)], nx, lmu)[seq(ninmax), , drop = FALSE] df = apply(abs(ca) > 0, 2, sum) ja = fit$ia[seq(ninmax)] oja = order(ja) ja = rep(ja[oja], lmu) ia = cumsum(c(1, rep(ninmax, lmu))) # beta に格納する beta = drop0(new("dgCMatrix", Dim = dd, Dimnames = list(vnames, stepnames), x = as.vector(ca[oja, ]), p = as.integer(ia - 1), i = as.integer(ja - 1))) } else { beta = zeromat(nvars, lmu, vnames, stepnames) df = rep(0, lmu) } # ここも省略 list(a0 = a0, beta = beta, df = df, dim = dd, lambda = lam) }
これにいくつかの情報を追加したものがglmnetの返り値です。elnet1において評価されたaがaoに格納され、elnetにcaとして渡され、elnet.rでbetaに抽出・格納される流れが伝わりましたでしょうか。
重要な変数を説明したところなので、以下ブロックで初期化している変数の詳細は出てきたときに説明するとして、さっさと次に進んでしまいましょう。
mm=0 nlp=0 nin=nlp iz=0 mnl=min(mnlam,nlam)
ループ①(almの更新)
上記までで必要な変数の初期化が完了したので、以下よりループに入ります。
一番外側のループはlambdaの個数(nlam)に対して実行されますが、nlamのデフォルトは 100 となっています(glmnet.r)。
以下ではおおよそalmを更新する処理を行うのですが、lambdaの指定の有無や、ループの回数によってalmに入力する値を変えています。
まずはlambdaの指定の有無で処理を分けます。以下のまとまりはflminが 1.0 より小さい場合にスキップされますが、先ほど述べたように、flminはglmnet.rにおいてlambdaの指定がない場合に相当します。
lambdaの指定がある場合にはalm = ulam(m)としてalmを更新した上で、10291 までスキップするのですが、この 10291 は 2 番目のループの中にありますので、少し大きめのスキップとなるようです。
なおulamはlambdaが指定されている場合、lambdaの降順になっているため、ループの 1 回目であればlambdaの最大値が入ります。
do 10281 m=1,nlam ! nlambda なので lambda の個数だけループ if(itrace.ne.0) call setpb(m-1) ! プログレスバー if(flmin .lt. 1.0)goto 10301 alm=ulam(m) ! flmin が 1.0 以上の場合は alm = ulam(m) とする goto 10291
lambdaの指定がなければ以下の処理に入るのですが、ここではループの回数によってalmに入力する値を変えています。
具体的には、ループの 1 回目にはbig(9.9d35)という極端に大きな値を入力し、 2 回目には 0.0 を、3 回目以降は 元の値にalfを乗じたものを入力します。
10301 if(m .le. 2)goto 10311 ! ループの1回目と2回目はここをスキップ alm=alm*alf ! ループの3回目からは alm を alf を乗じる goto 10291 10311 if(m .ne. 1)goto 10321 ! ループの2回目はここをスキップ alm=big ! ループの1回目は alm = big(9.9d35) にする goto 10331 10321 continue alm=0.0 ! ループの2回目は alm を いったん 0 にする
このalfは先ほど説明した通りeqs^(1.0/(nlam-1))として定義されますが、eqsが 0.01 or 1e-4 とすると、nlambdaを 10 とした場合には以下のような数値になります:
0.01^(1/(10-1)) # [1] 0.5994843 1e-4^(1.0/(10-1)) # [1] 0.3593814
つまりalmはだんだん絶対値が小さくなるわけですね。
ループ②(罰則の定義)
続いて 2 番目のループに入ります…と言いつつ 2 番目のループは一瞬で終わります。
先ほど更新したalmについて変数ごとの内積と比較し、大きい方を採用します。
したがってここでは各変数に対するループとなります。
まずjuとvpですが、juは前回記事で確認した通り、chkvarsによって各変数列の内容が全く同じでないかを確認したものでした。
ある変数列の中身が全く同じであれば 0 であったため、ここで次の変数にスキップされます。
次にvpですが、これは 1 回目の記事で確認した通りglmnet.rにおいて各変数に対する罰則の重み(デフォルトは 1) が入ったベクトルとして定義されたものです(vp = as.double(penalty.factor))。
罰則をかけない場合は 0 となり、スキップされるようです。
変数にバラつきがあり、罰則を検討する場合にはここで再度almを更新します。
ここで出てくるgはstandardの中でyとxの内積(共分散)を格納したものとして定義されたものでした。
それを罰則の大きさで除しているため、penalty.factorを小さくする(分母が小さくなる)と共分散が大きくなり変数として残りやすい、というロジックになっているようですね。
ちなみにループ①の 1 回目のループはalmに 9.9d35 という数値が入るので必ずこの数値が採用されると思います。またループ 2 回目は今度はalmが 0.0 になるため、今度は必ず変数の共分散側の数値がalmになると思われます。
! 2番目のループ ! alm の更新 do 10341 j=1,ni ! ni は変数の数 if(ju(j).eq.0) goto 10341 if(vp(j).le.0.0) goto 10341 alm=max(alm,abs(g(j))/vp(j)) 10341 continue ! 2番目のループここまで
上記の処理で変数を横断してalmを更新したのち、以下でさらにalmを更新します。
ここではbta(alpha; L1 と L2 への重みの配分パラメータ)と 0.001 の max で alm を除し、alfを乗じています。
一応ここで式を確認しておくと以下のようになります:
一体これは何をやっているんでしょうか…。
continue alm=alf*alm/max(bta,1.0d-3)
続いていくつかの変数を更新します。
demはalm * ombとして定義されますが、ここでombは (1-bta)でした。 またabはalmにbtaを乗じたものですので、これらはそれぞれ「lambda×(1-alpha)」および「lambda×alpha」ということになり、demとabが実質的な罰則の大きさを表すことになりそうですね。
10331 continue 10291 continue dem=alm*omb ! dem = alm * (1-bta) ab=alm*bta ! ab = alm * bta
これらがどのように使われているか少し先を見てみましょう。
! ab u=g(k)+ak*xv(k) ! L69(ループ③の中)、L119(ループ⑥の中) v=abs(u)-vp(k)*ab ! L70、L120(ともに上に同じ) ! dem a(k)=0.0 ! L71、L121 if(v.gt.0.0) a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem))) ! L72、L122
両方ともvpに乗じており、abはabs(u)からの減算、demはxv(k)との加算の後にsign(v,u)と除算し、clとの max/min を取っています。
vpは罰則の重みを定義したものでしたので、alphaとlambdaで決まる罰則の大きさをそのまま使うか弱くするかを決めています。
demの方は演算の結果をaに格納していますが、前述の通りaは回帰係数を保存する変数でしたので、sign(v,u)/(xv(k)+vp(k)*dem)がcl(1,k)よりも大きければa、すなわち回帰係数が更新されるということになりますね。
またこの演算が実行されるかの基準としてvが使われており、このvを計算するためにabが使われている、ということのようです。
じゃあこのuとかvって何なの?という話なのですが、これは次のループの話なので少しお待ちください。
残る変数のうちrsq0は残差平方和ですね。またjzはizと組み合わせて使われていますが、この条件分岐がちょっと理解出来なかったのでスキップします。
一応、izはループ①の途中(ループ③が終了した時点)で 1 になるため、iz * jzが 0 になるのはほぼjzが 0 の時に限ると言えそうです。
nlpは iteration のカウンターとして使われており、dlxは回帰係数の更新前後の差分を見ています。
どちらもループを抜けるための基準として使われています。
rsq0=rsq jz=1 continue 10351 continue if(iz*jz.ne.0) goto 10360 ! iz = 0, jz = 1 nlp=nlp+1 dlx=0.0
ちょっと長くなってしまったので一度きります。 次回はループ③から始めます。
glmnetをもう少し理解したい③
前回の記事では R の関数 elnet の中で elnet という Fortran のサブルーチンが呼ばれ(やっぱりややこしいですね)、さらに type.gaussian の値( covariance と naive )によって elnetu と elnetn のいずれかが呼ばれるところまで確認しました。
今回は elnetu の中身を見ていきます。
過去の記事はこちらです。
elnetu の実装
それでは早速 elnetu を見ていきましょう。 elnetu は elnet と同様にそれほど大きくないのでいきなり内容の確認に入りますが、処理としては以下の手順になっているようです:
- 前処理
- 標準化
- フィッティング
- 後処理
まずは前処理ですが、メモリの割り付けのあとに chkvars というサブルーチンを呼び出しています。
subroutine elnetu(parm,no,ni,x,y,w,jd,vp,cl,ne,nx,nlam, flmin,ulam,thr,isd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) implicit double precision(a-h,o-z) double precision x(no,ni),y(no),w(no),vp(ni),ulam(nlam),cl(2,ni) double precision ca(nx,nlam),a0(nlam),rsq(nlam),alm(nlam) integer jd(*),ia(nx),nin(nlam) double precision, dimension (:), allocatable :: xm,xs,g,xv,vlam integer, dimension (:), allocatable :: ju allocate(g(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xm(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xs(1:ni),stat=jerr) if(jerr.ne.0) return allocate(ju(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xv(1:ni),stat=jerr) if(jerr.ne.0) return allocate(vlam(1:nlam),stat=jerr) if(jerr.ne.0) return ! 1. 前処理 call chkvars(no,ni,x,ju) if(jd(1).gt.0) ju(jd(2:(jd(1)+1)))=0 if(maxval(ju) .gt. 0)goto 10071 jerr=7777 return 10071 continue
この chkvars では x の各変数について一行目の値と異なる値が二行目以降にあるかを確認し、 ju に格納しています。
subroutine chkvars(no,ni,x,ju) implicit double precision(a-h,o-z) double precision x(no,ni) integer ju(ni) ! ここから各変数のチェックを開始 do 11061 j=1,ni ju(j)=0 t=x(1,j) ! 1行目の値を取得 ! ここから2行目の値を確認する do 11071 i=2,no ! t は x(1, j) なので、各変数 j について 1 行目の値と等しいかを確認している if(x(i,j).eq.t) goto 11071 ! 等しければ次の行へ ju(j)=1 ! 等しくない数値があれば ju を 1 にして次の変数へ goto 11072 11071 continue 11072 continue 11061 continue continue return end
異なる値がなければ全ての値は同じということになりますので、例えば回帰係数を推定する意味はありません。
後続の処理ではこの ju を参照してスキップするかを決めている箇所が多々出てきます。
続いて standard というサブルーチンを呼び出して標準化を行います。
! 2. 標準化 call standard(no,ni,x,y,w,isd,intr,ju,g,xm,xs,ym,ys,xv,jerr)
この standard とうサブルーチンは結構大きく見えますが、切片の有無で処理を分けているため重複部分があります。
処理の内容としては:
- 重みの変換
- y と x の更新
- y と x の内積(共分散)を計算
となっています。
まずは重みの変換を確認してみると、重み w を「重みの総和あたりの重み」に変換し、
さらにその平方根をとったものを v として定義しています。
またその次から、先に述べたように切片の有無によって処理を分けています。
subroutine standard(no,ni,x,y,w,isd,intr,ju,g,xm,xs,ym,ys,xv,jerr) implicit double precision(a-h,o-z) double precision x(no,ni),y(no),w(no),g(ni),xm(ni),xs(ni),xv(ni) integer ju(ni) double precision, dimension (:), allocatable :: v allocate(v(1:no),stat=jerr) if(jerr.ne.0) return ! 1. 重みの変換 w=w/sum(w) v=sqrt(w) ! intr は intercept なので切片が 0 であるかで判定 ! 切片が 0 でない場合は 10141 に飛ばされる if(intr .ne. 0) goto 10141
以降の処理ではこの v を y や x に対して掛け合わせるのですが、全ての観測値の重みが等しい単純なパターンを想定すると w には $1/n$ 、v にはその平方根が入ります。
例えば観測値の数が 100 であれば $w = 1/100 = 0.01$ 、$v = sqrt(1/100) = 0.1$ となります。
ではこのような w や v を使って何をやっているかというと、 y に対しては:
ということをしています。
! 2. y と x の更新 ! 以下のセクションでは y と x それぞれについて観測値の重みを使って色々と調整する ! まずは y ym = 0.0 y = v*y ys = sqrt(dot_product(y,y)-dot_product(v,y)**2) y = y/ys
ただこの説明だけでは意味が分からないと思いますので少し式を整理してみましょう。
もとの y および w を $y0$ 、 $w0$ とおくと、
となります。
また ys の二乗(平方根を取る前) $ (ys)^{2} $ は:
と書けます。
ここで $w$ は観測値に対する重み $w0$ をその総和で除した形(単純なパターンでは $\frac{1}{n}$ )となっていることを思い出すと、これを乗じたものの総和は重み付き平均となります。
そうすると右辺の第一項はもともとの y ($y0$)の二乗の重み付き平均、第二項は重み付き平均の二乗が得られていることがわかります。
二乗の平均から平均の二乗を引いたものと言えば分散ですので、その平方根をとった ys は $y0$ の重み付き標準偏差を得ているようです
(ところで $w$、$w0$ は添字 $i$ を付けるべきですが、はてなブログの LaTeX がなぜか崩れるので省略しています)。
実際にサンプルデータで計算してみましょう。 まずは以下のような簡単なデータで二乗の平均から平均の二乗を引いたものが分散になることを確認します。
# 適当なデータ a <- c(5, 5, 6, 7, 9) # 一般的な分散の計算 mean((a - mean(a))^2) # 二乗の平均から平均の二乗を引いてみる mean(a^2) - mean(a)^2 # R の var を使う var(a) * 4 / 5
[1] 2.24 [1] 2.24 [1] 2.24
上の例ではいずれも同じ値を返していることがわかります。
なお var を使った計算では不偏分散ではなく標本分散に修正しました。
続いて先の計算にしたがった場合に、やはり同じように分散・標準偏差が得られるかを見てみます。
set.seed(123) n <- 10 y0 <- rnorm(n) w0 <- rep(1, n) w <- w0/sum(w0) v <- sqrt(w) y <- v*y0 ys <- sqrt(y %*% y - (v %*% y)^2) y_new <- y/ys[1]
> mean((y0 - mean(y0))^2) # 一般的な分散の計算 [1] 0.8187336 > mean(y0^2) - mean(y0)^2 # 二乗の平均から平均の二乗を引く [1] 0.8187336 > var(y0) * (n-1) / n # R の var を使って [1] 0.8187336 > (ys^2)[1] # 計算した値 [1] 0.8187336
$(ys)^{2}$ が $y0$ の分散になっていることが確認できますね。
ということで、先ほどの処理では w や v を使ってもともとの y の重み付き標準偏差を計算し、その値で重み付きの y を除していることがわかりました。
このサブルーチンの名前が standard なので当然ですが、標準化をしているようです。
x についても基本的に同様の処理を行っており、v を使って重み付き標準偏差を計算・標準化をしています。
ただし最後に重み付き平均の二乗 / 分散 に 1 を加算したものを xv に格納しており、これを x の分散としているようなのですが、これが良くわかりませんでした。
ちなみに ju は先ほど説明したように各変数に異なる数値・バラつきがあるかを示すもので、バラつきがなければさっさとループを抜けて次の変数に移っていることがわかります。
! x do 10151 j=1,ni ! ni は nvars if(ju(j).eq.0)goto 10151 xm(j) = 0.0 x(:,j) = v*x(:,j) ! x にも重みを乗じる xv(j) = dot_product(x(:,j),x(:,j)) ! x の二乗の重み付き平均 ! isd は標準化するかの指定で、標準化する場合は 1 が入っており 10171 に飛ばされない if(isd .eq. 0) goto 10171 xbq = dot_product(v, x(:,j))**2 ! x の重み付き平均の二乗 vc = xv(j)-xbq ! 重み付き分散 xs(j) = sqrt(vc) ! 重み付き標準偏差。 ys と対応している。 x(:,j) = x(:,j)/xs(j) ! 標準偏差で割って標準化。 y/ys と対応している。 ! これはよくわからない xv(j) = 1.0 + xbq/vc ! 重み付き平均の二乗 / 分散 に 1 を加算 goto 10181 10171 continue xs(j)=1.0 10181 continue continue 10151 continue continue goto 10191
切片が 0 でない場合はこちらにきます(基本はこっち)が、処理は上記と大体同じです。
y、x ともに値を更新する前に重み付き平均を引いているところが違う点ですね。
! 切片が 0 でない場合ここに来る ! 基本はこっち 10141 continue ! x do 10201 j=1,ni if(ju(j).eq.0)goto 10201 xm(j) = dot_product(w,x(:,j)) ! x の重み付き平均 x(:,j) = v*(x(:,j)-xm(j)) ! 重み付き平均を引いてから重みを乗じる xv(j) = dot_product(x(:,j),x(:,j)) ! 二乗の重み付き平均 if(isd.gt.0) xs(j) = sqrt(xv(j)) ! 重み付き標準偏差 10201 continue continue if(isd .ne. 0)goto 10221 xs = 1.0 goto 10231 10221 continue do 10241 j=1,ni if(ju(j).eq.0)goto 10241 x(:,j) = x(:,j)/xs(j) ! 標準化はここで実行 10241 continue continue xv=1.0 10231 continue continue ym = dot_product(w,y) ! y の重み付き平均 y = v*(y-ym) ! y から重み付き平均を引いたものに重みを乗じる ys = sqrt(dot_product(y,y)) ! 二乗和(分散)の平方根(SD) y = y/ys ! 標準化
次の処理は共通のもので、y と x の内積を計算し、 g に格納します。
単純に y と x の内積を計算しているように見えますが、ここでの y は
、x は
となっているので、その内積は重み付き共分散をそれぞれの標準偏差の積で除したもの、つまり重み付きの相関係数となっているはずです。
! 3. 内積(重み付き相関係数)を格納 10191 continue continue g = 0.0 do 10251 j=1,ni ! j 番目の変数にバラツキがあるなら g に y と x の内積(共分散)を格納する ! ただしこの時点での y と x はそれぞれ標準偏差で除したものとなっている if(ju(j).ne.0) g(j) = dot_product(y, x(:,j)) 10251 continue continue deallocate(v) return end
先のサンプルデータで確かめてみましょう。
重みが全て等しいという単純なパターンでは、更新された y と x の内積が相関係数になっていることが確認できます。
set.seed(123) n <- 10 y0 <- rnorm(n) x0 <- rnorm(n) w0 <- rep(1, n) w <- w0/sum(w0) v <- sqrt(w) y <- v*(y0 - (w %*% y0)[1]) ys <- sqrt(y %*% y) y_new <- y/ys[1] x <- v*(x0 - (w %*% x0)[1]) xs <- sqrt(x %*% x) x_new <- x/xs[1]
> (y_new %*% x_new)[1] # 内積 [1] 0.5776151 > cor(y_new, x_new) # 更新後の y と xの相関係数 [1] 0.5776151 > cor(y0, x0) # 元の値の相関係数 [1] 0.5776151
一方重みが観測値によって異なる場合はというと、これは近い値になるものの完全に一致はしませんでした(でもこれなんでだろう、一致するような気がするんだけど)。
set.seed(123) n <- 10 y0 <- rnorm(n) x0 <- rnorm(n) w0 <- rep(1, n) - 0.5 * ifelse(runif(n) > 0.8, 1, 0) # 一部のデータに対して重みを小さくしている w <- w0/sum(w0) v <- sqrt(w) y <- v*(y0 - (w %*% y0)[1]) ys <- sqrt(y %*% y) y_new <- y/ys[1] x <- v*(x0 - (w %*% x0)[1]) xs <- sqrt(x %*% x) x_new <- x/xs[1]
> (y_new %*% x_new)[1] [1] 0.5687947 > cor(y_new, x_new) [1] 0.5687133 > cor(y0, x0) [1] 0.5776151
ところで重み調整後の y と x の内積が相関係数と近似(一致?)するなら、個別のデータのペアが相関に対してどのような影響を持っているかを評価できるのではないでしょうか。
内積ではなく各ペアの掛け算語の値を見てみると、6 番目と 8 番目の値が高い値を示していることがわかります。
このデータの重み付き相関係数は 0.568 ぐらいだったので、この 2 つの観測値の影響が大きそうです。
> cbind(1:n, y_new * x_new) [,1] [,2] [1,] 1 -0.0744142551 [2,] 2 -0.0043928887 [3,] 3 0.0261049036 [4,] 4 0.0004833048 [5,] 5 -0.0025033504 [6,] 6 0.2852904868 [7,] 7 0.0104270429 [8,] 8 0.3466035906 [9,] 9 -0.0413263433 [10,] 10 0.0225221645
実際にデータを見てみると、 6 番と 8 番のデータは他の観測値と比べて関連性が強そうに見えます。
> cbind(y_new, x_new) y_new x_new [1,] -0.233569767 0.31859541 [2,] -0.117117800 0.03750829 [3,] 0.513582873 0.05082900 [4,] -0.011106121 -0.04351698 [5,] 0.009617489 -0.26029149 [6,] 0.568708951 0.50164585 [7,] 0.126538479 0.08240215 [8,] -0.481982832 -0.71912020 [9,] -0.278126098 0.14858851 [10,] -0.136535493 -0.16495465
6 と 8 番目のデータを塗り分けてみるとわかりやすいですね。
cols <- c(1, 1, 1, 1, 1, 3, 1, 3, 1, 1) + 1 plot(y ~ x, col = cols, pch = 16)
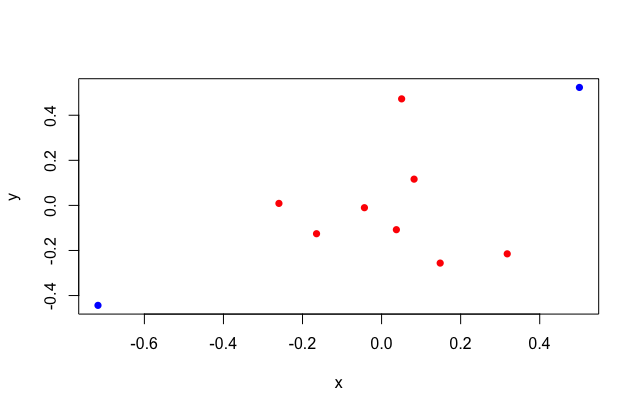
以上で y と x について標準化が終わったのでstandard から elnet に帰ってくると今度は回帰係数の上限・下限についても標準化を行います。
また flmin が 1 以上の場合は vlam を更新するのですが、 flmin は lambda が指定された場合に 1 が入り、そうでなければ $[0, 1)$ の実数が期待されるパラメータでした。
なので lambba が指定された場合(= flmin が 1 のとき)に vlam が y の重み付き標準偏差で調整される事になります。
この vlam は後続の処理(フィッティング)では ulam として渡されるものですが、ulam は lambda の指定がなければ 1 、指定があればその降順となるものでした。
要するに lambda の大きさについても標準化するよ、という事のようですね。
! jerr に 0 でない値が入っていると return if(jerr.ne.0) return ! cl は glmnet で cl = rbind(lower.limits, upper.limits) と定義される ! 回帰係数の上限・加減 cl=cl/ys ! 標準化の指定が 0 であれば以下はスキップ if(isd .le. 0) goto 10091 ! 説明変数ごとに標準偏差を乗じる do 10101 j=1,ni cl(:,j)=cl(:,j)*xs(j) 10101 continue continue 10091 continue ! flmin は glmnet のなかで flmin = as.double(lambda.min.ratio) で定義される ! ここで lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04) if(flmin.ge.1.0) vlam=ulam/ys
ではフィッティングです。
ここで呼ばれる elnet1 こそが {glmnet} の本体となり、回帰係数の計算はここで行われます。
この中ではもうサブルーチンはほとんど呼ばれず、初期パラメータを取ってくるものとプログレスバーを表示するためのものだけです。
ようやくたどり着きました、今回も長かったですね。
! 3. フィッティング ! 本体である elnet1 の呼び出し call elnet1(parm,ni,ju,vp,cl,g,no,ne,nx,x,nlam,flmin,vlam,thr,maxi,xv, lmu,ca,ia,nin,rsq,alm,nlp,jerr)
このサブルーチンは量はそこそこ(180行程度)なのですが、ループが込み入っていて紹介が長くなるので今回はここまでです。 また次回。
glmnetをもう少し理解したい②
前回の記事では glmnet の中身を確認し、引数の family によって呼び出す関数を変えていることがわかりました。
今回はそのなかでも gaussian が指定された場合の関数である elnet を見ていきましょう。
なお前回の記事はこちらです。
elnet の実装
それでは早速 elnet という関数を見ていきましょう。
ちなみにここでの elnet はコンソールで elnet と打っても表示されませんが、C や Fortran で書かれたものではなくて単に glmnet からエクスポートされていない関数なので glmnet:::elnet で中身を見ることができます。
この関数はそれほど長くないのでいきなり内容の確認に入りますが、他の多くの関数同様に elnet でも最初はパラメータの受け取り・確認を行います。
下のブロックでは反復回数( maxit )、観測値の重み( weights )を受け取った後、 type.gaussian の指定内容によって ka というパラメータに格納する値を変えています。
function (x, is.sparse, ix, jx, y, weights, offset, type.gaussian = c("covariance", "naive"), alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit) { # 1. パラメータの受け取り ### maxit maxit = as.integer(maxit) ### weights weights = as.double(weights) ### type.gaussian type.gaussian = match.arg(type.gaussian) ka = as.integer(switch(type.gaussian, covariance = 1, naive = 2, ))
ka はさらに先の処理で elnetu と elnetn という2つのサブルーチンのどちらを呼ぶかを決めていますので、 type.gaussian の指定に合わせてサブルーチンを変更しているということですね。
以下では y および offset (存在する場合)を double に変換しています。
また y の重み付き平均を使って Null Deviance (残差逸脱度)を計算しています。
### y の storage.mode storage.mode(y) = "double" ### offset if (is.null(offset)) { is.offset = FALSE } else { storage.mode(offset) = "double" is.offset = TRUE y = y - offset } ### 重み付き平均 ybar = weighted.mean(y, weights) ### Null Deviance(帰無モデルの残差逸脱度) nulldev = sum(weights * (y - ybar)^2) if (nulldev == 0) stop("y is constant; gaussian glmnet fails at standardization step")
次のブロックで早速フィッティングに入ります。
is.sparse が指定されているか否かで spelnet と elnet のどちらが呼ばれるかが決まりますが、引数の違いとしては spelnet において x が as.double とされており、 ix と jx (いずれも疎行列において非ゼロの要素の座標を特定するための数値)が追加されています。
# 2. フィッティング ## 疎行列であるかで関数を変える fit = if (is.sparse) .Fortran("spelnet", ka, parm = alpha, nobs, nvars, x, # 疎行列である場合、以下の ix, jx が引数として追加される # ix, jx は疎行列における非ゼロの要素の累積個数と行番号 ix, jx, y, weights, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, maxit, lmu = integer(1), a0 = double(nlam), ca = double(nx * nlam), ia = integer(nx), nin = integer(nlam), rsq = double(nlam), alm = double(nlam), nlp = integer(1), jerr = integer(1), PACKAGE = "glmnet") else .Fortran("elnet", ka, parm = alpha, nobs, nvars, as.double(x), y, weights, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, maxit, lmu = integer(1), a0 = double(nlam), ca = double(nx * nlam), ia = integer(nx), nin = integer(nlam), rsq = double(nlam), alm = double(nlam), nlp = integer(1), jerr = integer(1), PACKAGE = "glmnet") # nx は 非ゼロの変数の個数 # nlam は検証する lambda の個数 # なので ca は変数の数 * lambda の数
処理を抜けたあとは、エラーをチェックした上で必要なパラメータを取得します。
# 3. 後処理 ## エラーチェック if (fit$jerr != 0) { errmsg = jerr(fit$jerr, maxit, pmax = nx, family = "gaussian") if (errmsg$fatal) stop(errmsg$msg, call. = FALSE) else warning(errmsg$msg, call. = FALSE) } ## パラメータ(切片、回帰係数、自由度、次元、lambda)を取ってくる outlist = getcoef(fit, nvars, nx, vnames) ## パラメータ(xxxxxxxxxx)を取ってきて outlist に結合する dev = fit$rsq[seq(fit$lmu)] outlist = c(outlist, list(dev.ratio = dev, nulldev = nulldev, npasses = fit$nlp, jerr = fit$jerr, offset = is.offset)) ## elnet クラスを付与する class(outlist) = "elnet" outlist }
それでは次に elnet の本体である elnet(ややこしいですね) の中身を見ていきましょう。
elnet(二度目)の実装
上記のフィッティングのセクションで elnet は .Fortran("elnet") として呼ばれていました。これまで glm や GAM で見てきたときと同じように、 glmnet でもやはり fortran に行き着くようですね。
と言ってもここではまだ関数自体は大きくなく、下のように(コメント抜きで)30行程度で書かれています。
subroutine elnet(ka,parm,no,ni,x,y,w,jd,vp,cl,ne,nx,nlam, flmin,u *lam,thr,isd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) implicit double precision(a-h,o-z) double precision x(no,ni),y(no),w(no),vp(ni),ca(nx,nlam),cl(2,ni) double precision ulam(nlam),a0(nlam),rsq(nlam),alm(nlam) integer jd(*),ia(nx),nin(nlam) double precision, dimension (:), allocatable :: vq; ! vp が 0.0 だった場合には jerr = 100000 として return してしまう if(maxval(vp) .gt. 0.0)goto 10021 jerr=10000 return 10021 continue allocate(vq(1:ni),stat=jerr) ! ここでも jerr に 0 以外の数値が入っていたら return してしまう if(jerr.ne.0) return ! vp の値によって vq を生成 ! デフォルトは 1 ! ni は nvars で変数の数なので、 vq にはデフォルトでは変数の数が入る ! でもなんで sum(vq) なんだろ vq=max(0d0,vp) vq=vq*ni/sum(vq) ! elnetu か elnetn のどちらを呼ぶかは ka .ne. 1 であるかで判断している ! 1 でなければ elnetn 、 1 なら elnetu if(ka .ne. 1)goto 10041 call elnetu (parm,no,ni,x,y,w,jd,vq,cl,ne,nx,nlam,flmin,ulam,thr, *isd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) goto 10051 10041 continue call elnetn (parm,no,ni,x,y,w,jd,vq,cl,ne,nx,nlam,flmin,ulam,thr,i *sd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) 10051 continue continue deallocate(vq) return end
goto を多用していますね。。。
変数宣言以下で気になるところとしては、 vp が 0 だったときの挙動と、 elnetu を呼ぶところでしょうか。
vp は前回の記事で確認した通り、 glmnet のなかで vp = as.double(penalty.factor) として定義されています。
この penalty.factor はデフォルトでは 1 が入りますので基本的には goto 10021 で飛ばされてしまいます。
このセクションで引っかかるのは明示的に penalty.factor に 0 を指定した場合ですね。
! vp は各変数に対する罰則の重み(デフォルトは 1) が入ったベクトル ! vp = as.double(penalty.factor) ! jerr の数値で後続の処理で出力するエラーメッセージが決まる if(maxval(vp) .gt. 0.0)goto 10021 jerr=10000 return 10021 continue allocate(vq(1:ni),stat=jerr)
では penalty.factor に 0 を指定した場合はどうなるかと言うと、 jerr に 10000 が入力されて return されます。
この jerr は先ほど確認した後処理において errmsg = jerr(fit$jerr, maxit, pmax = nx, family = "gaussian") としてエラーメッセージに変換されるのでした。
またこの jerr という関数は glmnet で定義されていますので、
> glmnet:::jerr function (n, maxit, pmax, family) { if (n == 0) list(n = 0, fatal = FALSE, msg = "") else { errlist = switch(family, gaussian = jerr.elnet(n, maxit, pmax), binomial = jerr.lognet(n, maxit, pmax), multinomial = jerr.lognet(n, maxit, pmax), poisson = jerr.fishnet(n, maxit, pmax), cox = jerr.coxnet(n, maxit, pmax), mrelnet = jerr.mrelnet(n, maxit, pmax)) names(errlist) = c("n", "fatal", "msg") errlist$msg = paste("from glmnet Fortran code (error code ", n, "); ", errlist$msg, sep = "") errlist } }
として取り出せます。
関数をみてみると、 errlist は switch(family, ~) で更に異なる関数を呼び出し、その結果を格納しているようです。
そのため更に jerr.elnet を確認すると
> glmnet:::jerr.elnet function (n, maxit, pmax) { if (n > 0) { if (n < 7777) msg = "Memory allocation error; contact package maintainer" else if (n == 7777) msg = "All used predictors have zero variance" else if (n == 10000) msg = "All penalty factors are <= 0" else msg = "Unknown error" list(n = n, fatal = TRUE, msg = msg) } else if (n < 0) { if (n > -10000) msg = paste("Convergence for ", -n, "th lambda value not reached after maxit=", maxit, " iterations; solutions for larger lambdas returned", sep = "") if (n < -10000) msg = paste("Number of nonzero coefficients along the path exceeds pmax=", pmax, " at ", -n - 10000, "th lambda value; solutions for larger lambdas returned", sep = "") list(n = n, fatal = FALSE, msg = msg) } }
else if (n == 10000) msg = "All penalty factors are <= 0" と、罰則項が 0 であることを教えてくれていますね。
さて続いて elnetu の呼びだしを確認すると、elnetu と elnetn のいずれを呼ぶかは ka で決まっています。
先ほど少し触れた通り、 ka は ka = as.integer(switch(type.gaussian, covariance = 1, naive = 2, )) で定義されています。
また type.gaussian は glmnet の引数であり、type.gaussian = ifelse(nvars < 500, "covariance", "naive") と定義されています。
変数の数が 500 未満であれば covarinace となり、 ka には 1 が引き渡されるので if(ka .ne. 1) には該当せず、したがって elnetu が呼ばれることになるようですね。
! elnetu か elnetn のどちらを呼ぶかは ka .ne. 1 であるかで判断している ! 1 でなければ elnetn 、 1 なら elnetu ! ka は elnet の第一引数 ! ka = as.integer(switch(type.gaussian, covariance = 1, naive = 2, )) ! この covariance / naive は変数の数で決まる ! type.gaussian = ifelse(nvars < 500, "covariance", "naive") if(ka .ne. 1)goto 10041 call elnetu (parm,no,ni,x,y,w,jd,vq,cl,ne,nx,nlam,flmin,ulam,thr, *isd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) goto 10051 10041 continue call elnetn (parm,no,ni,x,y,w,jd,vq,cl,ne,nx,nlam,flmin,ulam,thr,i *sd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr)
次回はこの elnetu を見てみましょう。
glmnetをもう少し理解したい①
久しぶりの更新です(いつも言っています)。
背景
データサイエンス入門シリーズの「スパース回帰分析とパターン認識」を読んでいたら大変面白かったので、いつものように glmnet の中身を見てみることにしました。
なお私は業務でLasso/Ridgeを使った経験があまりないため理解が間違っているかもしれませんが、その点あらかじめご了承ください。
こちらの本です。良い本です。
glmnet の実行結果
前回の GAM の時と同様に、まずは glmnet でどのような結果を得ることができるのか確認してみましょう。「スパース回帰分析とパターン認識」(以下、教科書)P12 コード1.2を(少し改変して)実行してみます。
なおこれらのコードはこちらからダウンロードすることもできます。
環境は以下のような感じです。
> sessionInfo() R version 3.6.0 (2019-04-26) Platform: x86_64-apple-darwin15.6.0 (64-bit) Running under: macOS Mojave 10.14.6 Matrix products: default BLAS: /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib locale: [1] ja_JP.UTF-8/ja_JP.UTF-8/ja_JP.UTF-8/C/ja_JP.UTF-8/ja_JP.UTF-8 attached base packages: [1] stats graphics grDevices utils datasets methods base loaded via a namespace (and not attached): [1] compiler_3.6.0 tools_3.6.0 grid_3.6.0 lattice_0.20-38
library(glmnet) library(plotmo) x <- scale(LifeCycleSavings[, 2:5]) y <- LifeCycleSavings[, 1] - mean(LifeCycleSavings[, 1]) lasso <- glmnet(x, y, family = "gaussian", alpha = 1) # alpha = 1 で lasso ridge <- glmnet(x, y, family = "gaussian", alpha = 0) # alpha = 0 で ridge ## directoryは適当に指定 png("./Image/glmnet_dive_01_01.png", width = 600, height = 400) plot_glmnet(lasso, xvar = "lambda", label = TRUE) dev.off() png("./Image/glmnet_dive_01_02.png", width = 600, height = 400) plot_glmnet(ridge, xvar = "lambda", label = TRUE) dev.off()
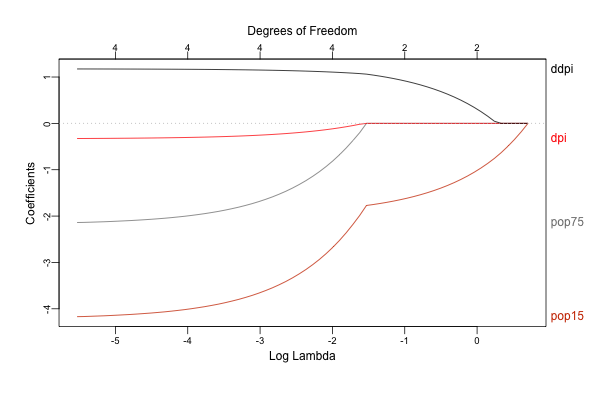
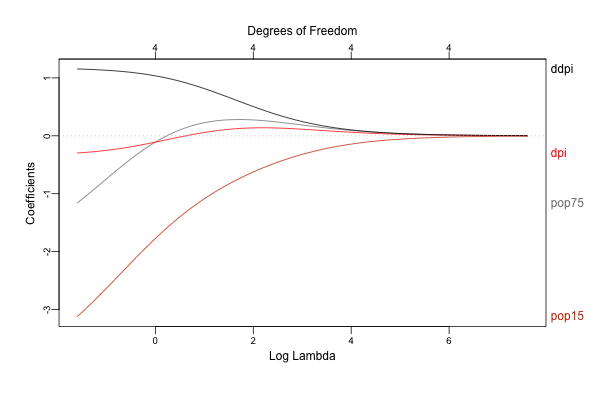
結果の解釈などについて詳しくは教科書を見て頂くとして、 glmnet は目的関数に回帰係数の規模に応じた罰則を設けることで、回帰係数を0に向かって縮小させながらフィッティングを行います。
またグラフのように罰則の大きさを色々と動かすことで各変数への回帰係数がどのように変化するかを評価することができます。
このグラフでは左から右に向かって罰則が強くなりますが、それにつれてLasso/Ridgeの両方とも回帰係数が0に向かって小さくなっている(縮小している)ことがわかります。
なお Lasso では回帰係数が0に収束している一方、 Ridge では微小ながら最後まで係数が0とならずに残っていることがわかりますが(グラフ上部の Degrees of Freedom が 4 のままとなっています)、 Lasso のように一部の回帰係数を正確に 0 と推定することが可能な手法をスパース推定と呼びます。
glmnet の実装
それでは glmnet という関数がどのように実装されているのか見ていきましょう。
まずはいつものように全体を眺め、見通しをよくします。
function (x, y, family = c("gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian"), weights, offset = NULL, alpha = 1, nlambda = 100, lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04), lambda = NULL, standardize = TRUE, intercept = TRUE, thresh = 1e-07, dfmax = nvars + 1, pmax = min(dfmax * 2 + 20, nvars), exclude, penalty.factor = rep(1, nvars), lower.limits = -Inf, upper.limits = Inf, maxit = 1e+05, type.gaussian = ifelse(nvars < 500, "covariance", "naive"), type.logistic = c("Newton", "modified.Newton"), standardize.response = FALSE, type.multinomial = c("ungrouped", "grouped"), relax = FALSE, trace.it = 0, ...) { ### 1. パラメータの設定、前処理、エラーチェック family = match.arg(family) if (alpha > 1) { warning("alpha >1; set to 1") alpha = 1 } if (alpha < 0) { warning("alpha<0; set to 0") alpha = 0 } alpha = as.double(alpha) this.call = match.call() nlam = as.integer(nlambda) y = drop(y) np = dim(x) if (is.null(np) | (np[2] <= 1)) stop("x should be a matrix with 2 or more columns") nobs = as.integer(np[1]) if (missing(weights)) weights = rep(1, nobs) else if (length(weights) != nobs) stop(paste("number of elements in weights (", length(weights), ") not equal to the number of rows of x (", nobs, ")", sep = "")) nvars = as.integer(np[2]) dimy = dim(y) nrowy = ifelse(is.null(dimy), length(y), dimy[1]) if (nrowy != nobs) stop(paste("number of observations in y (", nrowy, ") not equal to the number of rows of x (", nobs, ")", sep = "")) vnames = colnames(x) if (is.null(vnames)) vnames = paste("V", seq(nvars), sep = "") ne = as.integer(dfmax) nx = as.integer(pmax) if (missing(exclude)) exclude = integer(0) if (any(penalty.factor == Inf)) { exclude = c(exclude, seq(nvars)[penalty.factor == Inf]) exclude = sort(unique(exclude)) } if (length(exclude) > 0) { jd = match(exclude, seq(nvars), 0) if (!all(jd > 0)) stop("Some excluded variables out of range") penalty.factor[jd] = 1 jd = as.integer(c(length(jd), jd)) } else jd = as.integer(0) vp = as.double(penalty.factor) internal.parms = glmnet.control() if (internal.parms$itrace) trace.it = 1 else { if (trace.it) { glmnet.control(itrace = 1) on.exit(glmnet.control(itrace = 0)) } } if (any(lower.limits > 0)) { stop("Lower limits should be non-positive") } if (any(upper.limits < 0)) { stop("Upper limits should be non-negative") } lower.limits[lower.limits == -Inf] = -internal.parms$big upper.limits[upper.limits == Inf] = internal.parms$big if (length(lower.limits) < nvars) { if (length(lower.limits) == 1) lower.limits = rep(lower.limits, nvars) else stop("Require length 1 or nvars lower.limits") } else lower.limits = lower.limits[seq(nvars)] if (length(upper.limits) < nvars) { if (length(upper.limits) == 1) upper.limits = rep(upper.limits, nvars) else stop("Require length 1 or nvars upper.limits") } else upper.limits = upper.limits[seq(nvars)] cl = rbind(lower.limits, upper.limits) if (any(cl == 0)) { fdev = glmnet.control()$fdev if (fdev != 0) { glmnet.control(fdev = 0) on.exit(glmnet.control(fdev = fdev)) } } storage.mode(cl) = "double" isd = as.integer(standardize) intr = as.integer(intercept) if (!missing(intercept) && family == "cox") warning("Cox model has no intercept") jsd = as.integer(standardize.response) thresh = as.double(thresh) if (is.null(lambda)) { if (lambda.min.ratio >= 1) stop("lambda.min.ratio should be less than 1") flmin = as.double(lambda.min.ratio) ulam = double(1) } else { flmin = as.double(1) if (any(lambda < 0)) stop("lambdas should be non-negative") ulam = as.double(rev(sort(lambda))) nlam = as.integer(length(lambda)) } is.sparse = FALSE ix = jx = NULL if (inherits(x, "sparseMatrix")) { is.sparse = TRUE x = as(x, "CsparseMatrix") x = as(x, "dgCMatrix") ix = as.integer(x@p + 1) jx = as.integer(x@i + 1) x = as.double(x@x) } if (trace.it) { if (relax) cat("Training Fit\n") pb <- createPB(min = 0, max = nlam, initial = 0, style = 3) } kopt = switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) if (family == "multinomial") { type.multinomial = match.arg(type.multinomial) if (type.multinomial == "grouped") kopt = 2 } kopt = as.integer(kopt) ### 2. フィッティング fit = switch(family, gaussian = elnet(x, is.sparse, ix, jx, y, weights, offset, type.gaussian, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), poisson = fishnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), binomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), multinomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), cox = coxnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, vnames, maxit), mgaussian = mrelnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, jsd, intr, vnames, maxit)) if (trace.it) { utils::setTxtProgressBar(pb, nlam) close(pb) } ### 3. 後処理 if (is.null(lambda)) fit$lambda = fix.lam(fit$lambda) fit$call = this.call fit$nobs = nobs class(fit) = c(class(fit), "glmnet") if (relax) relax.glmnet(fit, x = x, y = y, weights = weights, offset = offset, lower.limits = lower.limits, upper.limits = upper.limits, check.args = FALSE, ...) else fit }
glmnet では以上のように、
- パラメータの設定、前処理、エラーチェック
- フィッティング
- 後処理
といったステップで処理が進んでおり、これは過去にみてきた glm や gam と同様ですね。
それでは各ステップを細かく見ていきましょう。
1. パラメータの設定、前処理、エラーチェック
まずはパラメータの設定や前処理に関わる部分ですが、はじめに family の指定が問題ないかをチェックします。
## 指定したfamilyが引数としてOKかチェック family = match.arg(family)
glmnet で使用可能な family は glm とは異なっており、Gamma / inverse.gaussian / quasi- が使えない代わりに、 multinomial / cox / mgaussian が使えるようになっています。
ここで multinomial は多項分布、mgaussian は多変量正規分布を意味するようです。
family のチェックには match.arg 関数が使われています。
この関数の挙動を理解するのは少し難しいのですが、こちらのブログが参考になります。
続いて alpha をチェックします:
## alpha ### LassoとRidgeそれぞれに対するペナルティの配分を決めるパラメータ ### glmnetにおける罰則項は以下で定義 ### alphaは0~1で、1ならLasso、0ならRidgeに対応 if (alpha > 1) { warning("alpha >1; set to 1") alpha = 1 } if (alpha < 0) { warning("alpha<0; set to 0") alpha = 0 } alpha = as.double(alpha)
glmnet においてこの alpha は、回帰係数のL1およびL2ノルムそれぞれに対する罰則の割合をコントロールします。
より具体的には、 glmnet では罰則項は以下によって定義されます(https://cran.r-project.org/web/packages/glmnet/glmnet.pdf の P19より):
冒頭のコードでは alpha = 1 または alpha = 0 としましたが、上の式から alpha = 1 のときにL2ノルムに対する罰則が消えてL1ノルムのみが残り(Lasso)、逆に alpha = 0 とするとL1ノルムに対する罰則が消えてL2ノルムが残る(Ridge)ことがわかります。
また alpha を (0, 1) とすると両者がそれぞれの割合でブレンドされます。
なお、ここでL2ノルムに対する罰則が1/2になっている理由はよくわかりませんでした。
glmnet の help で引用されているこちらの論文ではすでに $(1-\alpha)1/2||\beta||^2_2$ として定義されています。
またscikit-learnでも同様にL2ノルムに対しては0.5を乗じているようです(https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html)。
誰か理由を教えてください。
続いて match.call() を用いて引数の指定を正式なものに直します:
## match.call this.call = match.call()
これだけだと何を言っているかちょっとわからないと思いますので、以下の例で確認してみましょう:
myfun <- function(abc, def, ghi) { return(abc + 2*def + 3*ghi) }
上のように引数として abc 、 def 、 ghi を取る関数を定義します。
このとき R では、引数の指定がない場合には順番通りに入力されます:
> myfun(1, 2, 3) [1] 14
一部の引数のみ指定がある場合では指定された引数だけがその通りに入力され、残りは順番通りに割り当てられるようです。
> myfun(def = 3, 4, 5) [1] 25
ところでこの引数の指定は、一意に決まれば指定は省略することができます:
> myfun(d = 3, 4, 5) [1] 25
一方、例えば以下のような呼び出しでは g から始まる引数が2つあるため一意に決まらず、エラーとなってしまいます。
> myfun2 <- function(abc, def, ghi, gjk) { + return(abc + 2*def + 3*ghi + 4*gjk) + } > myfun2(g = 3, 4, 5, 6) myfun2(g = 3, 4, 5, 6) でエラー: 引数 1 が複数の仮引数に一致します
では match.call を使って関数を呼び出すとどうなるかと言うと:
> match.call(myfun, call("myfun", 1, def = 3, ghi = 5)) myfun(abc = 1, def = 3, ghi = 5)
この通り、各引数に対して何を割り当てたかを得ることができます。 便利ですね。
さらに続いて、 nlambda の指定です。
ここでは $\lambda$ (罰則の大きさ)そのものではなく、検証する $\lambda$ の数(nubmer of lambda)を指定します(デフォルトは100)。
## nlambda nlam = as.integer(nlambda)
ここからは y 、 x および weight のチェックです:
## drop y = drop(y) ## x ### x は2列以上持つ必要があるので、単回帰はできない様子 np = dim(x) if (is.null(np) | (np[2] <= 1)) stop("x should be a matrix with 2 or more columns") ### x のレコード数 nobs = as.integer(np[1]) ### weights ### 未入力のときは 1 を与え、weights と nobs が一致しないときはエラー if (missing(weights)) weights = rep(1, nobs) else if (length(weights) != nobs) stop(paste("number of elements in weights (", length(weights), ") not equal to the number of rows of x (", nobs, ")", sep = "")) ### 変数の数 nvars = as.integer(np[2]) ## y dimy = dim(y) ### y のレコード数 nrowy = ifelse(is.null(dimy), length(y), dimy[1]) ### y と x でレコード数が合わないときはエラー if (nrowy != nobs) stop(paste("number of observations in y (", nrowy, ") not equal to the number of rows of x (", nobs, ")", sep = "")) ## 変数名 vnames = colnames(x) if (is.null(vnames)) vnames = paste("V", seq(nvars), sep = "")
y に対する drop ですが、これは length が 1 であるような冗長な次元を落とす関数です。
続いて x の行数が weight や y と合わない場合にエラーを返しています。
以下ではモデルに含める変数や非ゼロとする変数などを指定します
( nx(=pmax) の方はちょっと理解がアヤシイので help の説明を書いておきます):
## 自由度 ### モデルに含まれる変数の上限を指定 ### dfmax = nvars + 1 ne = as.integer(dfmax) ### 非ゼロとする変数の数の上限(?) ### Limit the maximum number of variables ever to be nonzero ### pmax = min(dfmax * 2 + 20, nvars) nx = as.integer(pmax) ### 除外対象となる変数の指定 if (missing(exclude)) exclude = integer(0)
次に変数ごとに異なるペナルティを与えるために penalty.factor を指定します。
この数値が lambda に乗じられるため、例えば特定の変数に対して penalty.factor = 0 としておけば罰則を与えないようにすることが可能となります(結果として常にモデルに採用されるようになる):
## 変数ごとに異なるペナルティを与える ### デフォルトは 1 が入る ### Inf が指定されている変数は exclude として扱われる if (any(penalty.factor == Inf)) { exclude = c(exclude, seq(nvars)[penalty.factor == Inf]) exclude = sort(unique(exclude)) } if (length(exclude) > 0) { jd = match(exclude, seq(nvars), 0) if (!all(jd > 0)) stop("Some excluded variables out of range") penalty.factor[jd] = 1 jd = as.integer(c(length(jd), jd)) } else jd = as.integer(0) vp = as.double(penalty.factor)
これはせっかくなので実際にやってみましょう。
冒頭のコードを持ってきて、以下のように lambda を適当に設定してみます。
x <- scale(LifeCycleSavings[, 2:5]) y <- LifeCycleSavings[, 1] - mean(LifeCycleSavings[, 1])
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3)) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 1.182354e-15 pop15 -1.691002e+00 pop75 . dpi . ddpi 9.816514e-01
このとき、2・3番目の変数である pop75 と dpi は 0 と推定されてしまいました。
ここでこれらの変数の penalty.factor を 0 とすると
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3, + penalty.factor = c(1, 0, 0, 1))) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 9.523943e-16 pop15 -7.827680e-01 pop75 8.127991e-01 dpi -1.560908e-01 ddpi 6.812498e-01
ちゃんと推定されるようになっています。
逆に pop15 の penalty.factor を大きくすると
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3, + penalty.factor = c(2, 0, 0, 1))) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 7.266786e-16 pop15 . pop75 1.374655e+00 dpi 2.586151e-02 ddpi 9.300500e-01
このようにモデルから除外されることになります。
さらに penalty.factor = Inf とすると、その変数は exclude として扱われるようになります。
続いて glmnet.control で持っているパラメータを渡します。
## 内部でデフォルトで持っているパラメータ internal.parms = glmnet.control() ### プログレスバーを表示する! if (internal.parms$itrace) trace.it = 1 else { if (trace.it) { glmnet.control(itrace = 1) on.exit(glmnet.control(itrace = 0)) } }
次に、回帰係数に対する上限・下限を設定します。 なお下限は non-positive 、上限は non-negative しか設定できないようですね。
## 上限・下限 ### lower.limit としては非正の値のみ指定できる if (any(lower.limits > 0)) { stop("Lower limits should be non-positive") } ### upper.limtit は逆に非負の値のみ指定できる if (any(upper.limits < 0)) { stop("Upper limits should be non-negative") } ### Inf (デフォルト)になっているものについては特定の値(9.9e35)に差し替え lower.limits[lower.limits == -Inf] = -internal.parms$big upper.limits[upper.limits == Inf] = internal.parms$big ### nvars との整合性チェック if (length(lower.limits) < nvars) { ### lower.limits としてスカラが指定されている場合は nvars 全てに適用 if (length(lower.limits) == 1) lower.limits = rep(lower.limits, nvars) else stop("Require length 1 or nvars lower.limits") } ### lower.limits が nvars よりも長い場合は前から利用する else lower.limits = lower.limits[seq(nvars)] ### nvars との整合性チェック(lower.limits と同様) if (length(upper.limits) < nvars) { if (length(upper.limits) == 1) upper.limits = rep(upper.limits, nvars) else stop("Require length 1 or nvars upper.limits") } else upper.limits = upper.limits[seq(nvars)] ### 上限・下限 ### coefficient limit? cl = rbind(lower.limits, upper.limits) ### lower または upper に 0 を含む場合 ### 0除算が発生するときのエラー対策? if (any(cl == 0)) { ### fdev は最小となるデビアンスの変化量(割合) ### minimum fractional change in deviance for stopping path; factory default = 1.0e5 fdev = glmnet.control()$fdev if (fdev != 0) { glmnet.control(fdev = 0) on.exit(glmnet.control(fdev = fdev)) # 関数終了時に実行される処理 } } storage.mode(cl) = "double"
標準化と切片に対する指定です。 標準化の処理そのものは以降の関数の内部で実行されるため、ここでは指定のみを行います。
## 標準化 ### standardize と intercept はデフォルトは TRUE なので 1 になる isd = as.integer(standardize) intr = as.integer(intercept) ### Cox回帰における警告 if (!missing(intercept) && family == "cox") warning("Cox model has no intercept") ### standardize.response は family="mgaussian" のときに目的変数を標準化するかの指定 jsd = as.integer(standardize.response)
収束を判定する閾値を指定します。
## 収束判定 ### coordinate descent における収束の閾値 thresh = as.double(thresh)
次に、 lambda に関する指定となりますが、 flmin および ulam の使われ方がよく理解できなかったため、これらの説明は省略します。
なお help にもありますが、通常は lambda には単一の値ではなく、候補となる値のベクトルを与えます。
Avoid supplying a single value for lambda (for predictions after CV use predict() instead).
## lambda ### ペナルティの大きさ ### 指定がない場合、flmin と ulam は lambda.min.ratio および 1 に指定される ### lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04) if (is.null(lambda)) { if (lambda.min.ratio >= 1) stop("lambda.min.ratio should be less than 1") flmin = as.double(lambda.min.ratio) ulam = double(1) } ### 指定がある場合、flmin(下限?)とulam(上限?)は 1 および lambdaの降順 に指定される else { flmin = as.double(1) if (any(lambda < 0)) stop("lambdas should be non-negative") ulam = as.double(rev(sort(lambda))) nlam = as.integer(length(lambda)) }
次に疎行列の指定です。
入力 X が疎行列である場合、dgCMatrix 形式に変換されます。
ここで dgCMatrix とは列方向の志向性を持つ疎行列の形式です。
## sparse matrix ### x が Matrix::sparseMatrix の場合は Matrix::dgCMatrix に変換する ### dgCMatrix: csc順に並び替えて(csc形式)の疎行列圧縮保管 is.sparse = FALSE ix = jx = NULL if (inherits(x, "sparseMatrix")) { is.sparse = TRUE x = as(x, "CsparseMatrix") x = as(x, "dgCMatrix") ### x@p は各列の非ゼロの値の個数を積み上げたものが格納されている(列数 + 1) ### diff(x@p + 1) すれば各列の非ゼロの値の個数がわかる ix = as.integer(x@p + 1) ### x@i は各列の非ゼロの値の行番号が格納されている(なので length(x@i) が非ゼロの値の個数と一致する) ### 0-index なので R のスタイルと合わせるために +1 しているのでしょう jx = as.integer(x@i + 1) ### x@x は非ゼロである値そのもののベクトル x = as.double(x@x) }
ここも、せっかくなので疎行列における数値の格納方法についても見ておきましょう。 以下のように疎行列を作成します:
set.seed(1234) i <- c(1, 5, 18) j <- c(4, 13, 19) n <- rnorm(3) m <- matrix(0, 20, 20) for (k in 1:length(n)) { m[i[k], j[k]] <- n[k] } s_m <- as(m, "dgCMatrix")
ここで s_m は行列 m を疎行列として扱ったものです。
str() で確認すると、 s_m には
@ i:非ゼロの要素の入っていた行番号( 0-index であることに注意)@ p:各列における非ゼロの要素の個数を積み上げたもの@ Dim:行列の次元@ Dimnames:行列の各次元の名前@ x:非ゼロの要素の数値@ factors:(これはちょっとわかりませんでした)
が格納されています。
> str(s_m) Formal class 'dgCMatrix' [package "Matrix"] with 6 slots ..@ i : int [1:3] 0 4 17 ..@ p : int [1:21] 0 0 0 0 1 1 1 1 1 1 ... ..@ Dim : int [1:2] 20 20 ..@ Dimnames:List of 2 .. ..$ : NULL .. ..$ : NULL ..@ x : num [1:3] -1.207 0.277 1.084 ..@ factors : list()
ここで @ i には非ゼロである各要素の行番号が入るため行列 m を作ったときの行番号の指定 i に対応しますが、0-index であるため数字は1つずつ小さくなっています。
> print(i- 1) [1] 0 4 17 > print(s_m@i) [1] 0 4 17
ちょっとわかりにくいのが @ p で、ここには各列における非ゼロの要素の個数の累積が格納され、列数に対応します(ただし最初に 0 が追加されるため、列数 + 1 の長さになります)。
今回の例では行列の列数が 20 なので、length が 21 となります。
> length(s_m@p) [1] 21
このベクトルには非ゼロの要素の個数の累積が入っているため、差分を取ると元の行列で非ゼロの要素が入っていた列を得ることができます。
> diff(s_m@p) [1] 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0
列番号を指定した j と比較してみましょう:
> which(diff(s_m@p) == 1) [1] 4 13 19 > j [1] 4 13 19
合っていますね。
続く処理では、 ix には各列における非ゼロの要素の累積個数(+1)を
、 jx には行番号を代入しています。
また x には元の疎行列における非ゼロの要素の値そのものをベクトルとして入力しており、説明変数の行列が疎行列であった場合、この時点で行列ではなくベクトルとして扱われることになります。
次に、プログレスバーの指定です(出せるんですね)。
## プログレスバー if (trace.it) { if (relax) cat("Training Fit\n") pb <- createPB(min = 0, max = nlam, initial = 0, style = 3) }
そして最後に最適化の手法についての指定です。
family が `binomial または multinomial の場合、 glmnet の引数である type.logistic および type.multinomial が評価され、(後の工程で)それに応じて呼ばれる関数が変わります。
具体的には lognet2m 、 lognetn および multlognetn のどれが選ばれるかが決まります。
これは別の機会に解説します(予定です)。
## 最適化の手法(ロジスティックおよび多項ロジスティックの時) ### type.logistic = c("Newton", "modified.Newton") ### Newton を指定なら 0、modified.Newton を指定なら 1 を返す ### If "Newton" then the exact hessian is used (default), while "modified.Newton" uses an upper-bound on the hessian, and can be faster. kopt = switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) ### type.multinomial = c("ungrouped", "grouped") ### 多項ロジスティックで更にgroupedの場合は kopt は 2 となる ### If "grouped" then a grouped lasso penalty is used on the multinomial coefficients for a variable. This ensures they are all in our out together. ### The default is "ungrouped" if (family == "multinomial") { type.multinomial = match.arg(type.multinomial) if (type.multinomial == "grouped") kopt = 2 } kopt = as.integer(kopt)
最初の方で family のチェックに使われ、ここでも使われている match.arg ですが、せっかくなので挙動を確認しておきましょう:
### 引数に type.logistic を持つ関数を定義 myfun <- function(a = "aaa", type.logistic = c("Newton", "modified.Newton")) { ### 呼び出し元の関数の引数をチェックし、 Newton なら 0、modified.Newton なら 1を割り当てる kopt <- switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) kopt }
上のような関数を定義し、以下のように呼び出すと、結果はそれぞれ 0, 0, 1 となります。
> myfun() [1] 0 > myfun(type.logistic = "Newton") [1] 0 > myfun(type.logistic = "modified.Newton") [1] 1
2. フィッティング
以上でパラメータの設定や前処理が終わりましたので次はフィッティングです。
といってもここでは family に応じて呼び出す関数を変えているだけなので、詳細は一旦スキップしましょう。
# フィッティング ## family に応じてその後に呼び出す関数を変える fit = switch(family, ### gaussian のときは elnet gaussian = elnet(x, is.sparse, ix, jx, y, weights, offset, type.gaussian, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), ### poisson のときは fishnet poisson = fishnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), ### binomial のときは lognet binomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), ### multinomial のときも lognet multinomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), ### cox のときは coxnet cox = coxnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, vnames, maxit), ### mgaussian のときは mrelnet mgaussian = mrelnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, jsd, intr, vnames, maxit)) ## プログレスバー if (trace.it) { utils::setTxtProgressBar(pb, nlam) close(pb) }
なおここでそれぞれの関数に渡されている引数を比較すると以下のようになります(一部はよくわかりませんでした):
| 引数 | 説明 | elnet | fishnet | lognet | coxnet | mrelnet |
|---|---|---|---|---|---|---|
| x | 説明変数の行列 | 〇 | 〇 | 〇 | 〇 | 〇 |
| is.sparse | 疎行列であるかの指定 | 〇 | 〇 | 〇 | 〇 | 〇 |
| ix | 疎行列における非ゼロの要素の累積個数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jx | 疎行列における非ゼロの要素の行番号 | 〇 | 〇 | 〇 | 〇 | 〇 |
| y | 目的変数の行列 | 〇 | 〇 | 〇 | 〇 | 〇 |
| weights | 観測値に対する重み | 〇 | 〇 | 〇 | 〇 | 〇 |
| offset | オフセット | 〇 | 〇 | 〇 | 〇 | 〇 |
| type.gaussian | 1:covariance, 2:naïve | 〇 | - | - | - | - |
| alpha | L1とL2に対する重みの調整パラメータ | 〇 | 〇 | 〇 | 〇 | 〇 |
| nobs | レコード数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| nvars | 説明変数の数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jd | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| vp | 各変数に対する罰則の重み(penalty.factor) | 〇 | 〇 | 〇 | 〇 | 〇 |
| cl | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| ne | モデルに含まれる変数の上限。ne = dfmax = nvars + 1 | 〇 | 〇 | 〇 | 〇 | 〇 |
| nx | 非ゼロとする変数の個数の上限? | 〇 | 〇 | 〇 | 〇 | 〇 |
| nlam | lambdaの数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| flmin | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| ulam | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| thresh | 収束判定の閾値 | 〇 | 〇 | 〇 | 〇 | 〇 |
| isd | standardizeするかの指定 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jsd | ? | - | - | - | - | 〇 |
| intr | 切片(Intercept)を含めるかの指定 | 〇 | 〇 | 〇 | - | 〇 |
| vnames | 変数名 | 〇 | 〇 | 〇 | 〇 | 〇 |
| maxit | 反復回数の上限 | 〇 | 〇 | 〇 | 〇 | 〇 |
| kopt | 最適化の手法 | - | - | 〇 | - | - |
| family | family | - | - | 〇 | - | - |
3. 後処理
最後に後処理です。
# 後処理 ## lambda が指定されておらず fit$lambda が 3 パターン以上検証されている場合、先頭を差し替える ## glmnet::fix.lam ## function (lam) { ## if (length(lam) > 2) { ## llam = log(lam) ## lam[1] = exp(2 * llam[2] - llam[3]) ## } ## lam ## } if (is.null(lambda)) fit$lambda = fix.lam(fit$lambda) ## call fit$call = this.call ## レコード数 fit$nobs = nobs ## class に glmnet を追加 class(fit) = c(class(fit), "glmnet") # リターン ## relax が TRUE の場合、解パスの各セットについて罰則なしでモデルをフィッティングする ## If TRUE then for each active set in the path of solutions, the model is refit without any regularization. See details for more information. ## This argument is new, and users may experience convergence issues with small datasets, especially with non-gaussian families. ## Limiting the value of ’maxp’ can alleviate these issues in some cases. if (relax) relax.glmnet(fit, x = x, y = y, weights = weights, offset = offset, lower.limits = lower.limits, upper.limits = upper.limits, check.args = FALSE, ...) else fit
この後処理で目立つ工程としては relax の部分でしょう。
ここで relax は help によると、
If relax=TRUE a duplicate sequence of models is produced, where each active set in the elastic-net path is refit without regularization. The result of this is a matching "glmnet" object which is stored on the original object in a component named "relaxed", and is part of the glmnet output.
ということで、glmnet によって変数選択された結果を用いて、罰則なしで再度フィッティングを行うオプションのようです。
これも実際にやってみるのが早いと思いますので、以下のように実行してみます:
lasso_02 <- glmnet(x, y, family = "gaussian", relax = T)
すると、先程の結果( lasso )に、 lasso_02$relaxed という結果が追加されていることがわかりますが、内容は lasso とほとんど同じです。
> str(lasso) List of 12 $ a0 : Named num [1:68] 6.11e-16 6.71e-16 7.26e-16 7.76e-16 8.22e-16 ... ..- attr(*, "names")= chr [1:68] "s0" "s1" "s2" "s3" ... $ beta :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots .. ..@ i : int [1:216] 0 0 0 0 0 3 0 3 0 3 ... .. ..@ p : int [1:69] 0 0 1 2 3 4 6 8 10 12 ... .. ..@ Dim : int [1:2] 4 68 .. ..@ Dimnames:List of 2 .. .. ..$ : chr [1:4] "pop15" "pop75" "dpi" "ddpi" .. .. ..$ : chr [1:68] "s0" "s1" "s2" "s3" ... .. ..@ x : num [1:216] -0.181 -0.347 -0.497 -0.634 -0.757 ... .. ..@ factors : list() $ df : int [1:68] 0 1 1 1 1 2 2 2 2 2 ... $ dim : int [1:2] 4 68 $ lambda : num [1:68] 2.02 1.84 1.68 1.53 1.39 ... $ dev.ratio: num [1:68] 0 0.0352 0.0645 0.0888 0.1089 ... $ nulldev : num 984 $ npasses : int 562 $ jerr : int 0 $ offset : logi FALSE $ call : language glmnet(x = x, y = y, family = "gaussian", alpha = 1) $ nobs : int 50 - attr(*, "class")= chr [1:2] "elnet" "glmnet" > str(lasso_02$relaxed) List of 12 $ a0 : Named num [1:68] 6.11e-16 1.29e-15 1.29e-15 1.29e-15 1.29e-15 ... ..- attr(*, "names")= chr [1:68] "s0" "s1" "s2" "s3" ... $ beta :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots .. ..@ i : int [1:216] 0 0 0 0 0 3 0 3 0 3 ... .. ..@ p : int [1:69] 0 0 1 2 3 4 6 8 10 12 ... .. ..@ Dim : int [1:2] 4 68 .. ..@ Dimnames:List of 2 .. .. ..$ : chr [1:4] "pop15" "pop75" "dpi" "ddpi" .. .. ..$ : chr [1:68] "s0" "s1" "s2" "s3" ... .. ..@ x : num [1:216] -2.04 -2.04 -2.04 -2.04 -1.98 ... .. ..@ factors : list() $ df : int [1:68] 0 1 1 1 1 2 2 2 2 2 ... $ dim : int [1:2] 4 68 $ lambda : num [1:68] 2.02 1.84 1.68 1.53 1.39 ... $ dev.ratio: num [1:68] 0 0.208 0.208 0.208 0.208 ... $ nulldev : num 984 $ npasses : int 562 $ jerr : int 0 $ offset : logi FALSE $ call : language glmnet(x = x, y = y, family = "gaussian", relax = T) $ nobs : int 50 - attr(*, "class")= chr [1:2] "elnet" "glmnet"
ここで lasso_02$relaxed の中身を少し見てみると、例えば beta には以下のような数値が入っています。
> lasso_02$relaxed$beta[, 1:6] 4 x 6 sparse Matrix of class "dgCMatrix" s0 s1 s2 s3 s4 s5 pop15 . -2.040996 -2.040996 -2.040996 -2.040996 -1.980216 pop75 . . . . . . dpi . . . . . . ddpi . . . . . 1.270865
これは何かと言うと、少しずつ罰則の重みを変えたことで変数が選択された状態で通常の線形回帰を当てはめたときの回帰係数となっています。
例えば lasso_02$relaxed$beta[, 6] には、変数として選択された pop15 と ddpi それぞれの回帰係数が入っています。
実際に lm の結果と一致するか見てみましょう:
> coef(lm(y ~ x[, c(1, 4)])) (Intercept) x[, c(1, 4)]pop15 x[, c(1, 4)]ddpi 1.364331e-15 -1.980216e+00 1.270865e+00
合っていますね。
ところで切片の推定値が入っている lasso_02$relaxed$a0 の値は少し異なるようです:
> lasso_02$relaxed$a0[6] s5 1.28119e-15
なんでやろか。。
もしかしたら標準化の違いかとも思いましたがそれでもないようで、この理由はわかりませんでした。
lasso_03 <- glmnet(x, y, family = "gaussian", relax = T, standardize = F)
> lasso_03$relaxed$a0[6] s5 1.28119e-15
glmnet() の実装は以上となります。
次回はフィッティングの部分で呼ばれている elnet を詳しく見ていきましょう。
なお gam のときとは違い、 glmnet では library をインストールしてもソースコードは付いてきませんでしたので、こちらを参考に fortran のソースコードを取得しました。
ではまた次回。
統計数理研究所公開講座「統計の哲学を理解するために」参加記録
1/31に開催された統計数理研究所の公開講座「統計の哲学を理解するために」に参加してきましたのでそのメモを共有しておきます。全体的にはエリオット・ソーバーという尤度主義者から見た頻度主義・ベイズ主義に対する批判的観点の紹介という構成で、それぞれの立場が答えようとしている問いが浮き彫りになるような内容でした。
なおこの講義は「科学と証拠」という書籍に基づいています。とても面白い本です。

- 作者:エリオット・ソーバー
- 出版社/メーカー: 名古屋大学出版会
- 発売日: 2012/10/20
- メディア: 単行本
また最後に、あまり時間がなくて駆け足での紹介となっていましたが、Deborah Mayoによる「誤り統計学」について簡単に紹介がありました(松王先生曰く世界初の資料、とのこと)。

Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars
- 作者:Deborah G. Mayo
- 出版社/メーカー: Cambridge University Press
- 発売日: 2018/09/20
- メディア: ペーパーバック
日時
2020/1/31 10:00@立川
講師
北海道大学 松王政浩
エリオット・ソーバー
統計学論争は終わっていない
- Statistical Inference as Severe Testing
- Deborah Mayo
- 頻度主義
- Deborah Mayo
- 有意検定論争、レシピ的な統計学の食い止め
統計の哲学
- 統計の基礎をめぐる議論の総体
- 哲学は常に論争で成り立ち、結論には到達しない
- ベイズ主義
- 信念度合い
- 主観
- 客観
- 信念度合い
- 頻度主義
- ネイマン-ピアソン
- 無限回の施行を前提とした考えた
- フィッシャー
- 相対頻度、推測確率
- ネイマン-ピアソン
- ベイズ主義
- 統一的見解を示したものはないので各主義を学ぶしかない
3つの主義
- ロイヤルの3つの問い
- 証拠をもとに何がわかるか → 尤度主義
- 静的現在主義、外在主義
- データが直接示している「仮説に関する情報(証拠)」をキャッチせよ
- いったんデータが得られたら他のデータの可能性は捨象せよ
- 証拠をもとに何を信じるか → ベイズ主義
- 動的現在主義、内在主義
- 他のデータの可能性は一切捨象せよ
- データが「(可能な)仮説に関する情報」をどう変化させるかキャッチせよ
- 証拠をもとに何をするべきか → 頻度主義
- 反事実主義、規約主義
- この場で生じていることだけでなく、生じた可能性がある事柄もすべて併せて仮説について判断せよ
- 低い確率を棄却のサインとみなそう、同じルールを何度も適用すれば誤りの可能性が低いのだから今回もそのルールを適用する
- 証拠をもとに何がわかるか → 尤度主義
尤度「原理」について
- ソーバーの議論の核となる2つの原理
- 穏当な原理
- もしEが真であると知ることによって命題Pを棄却することが正当化され、かつ、この情報を得てはじめてPの棄却が正当化されたのであれば、EはPに反する証拠とされねばならない
- 全証拠の原理
- 実験によって得られたデータはすべて証拠の判断に用いられなければならない
- 穏当な原理
- 尤度の法則とは異なる
- 尤度主義、ベイズ主義の両方に共通する源泉
- 尤度原理(LP)
- xが観測されたあと、θについて推論(決定)する際に、実験について関係のあるすべての情報は、観測されたxに対する尤度関数に含まれている。さらに2つの尤度関数がθの関数として互いに比例の関係にあるなら2つの関数はθについて同じ情報を含んでいる
- フィッシャーに由来
- これを満たすか満たさないかで、陣営が分かれる
- 満たす
- 尤度主義、ベイズ主義
- 満たさない
- 頻度主義
- 満たす
- いまだ論争の火種
- もしLPがパラメータ推定の根本原理であるなら、
- P(x' | θi) = kP(x | θi) が成り立つときEv(E, x) = Ev(E', x')となるはず。Evは証拠、Eは実験
- これが成り立たなければそのような結果をもたらす推論は不適切
- バーンバウムが証明
- 証明の是非は未決着
- さらに遡ると
- 十分性の原理
- 条件付けの原理
- これら2つの原理は統計学者なら誰でも受け入れられるはずの原理
- これら2つの原理と尤度原理の等価性を「証明」(バーンバウム)、2つの原理を受け入れるなら尤度原理も受け入れないといけない
- バーンバウムの問題意識
- 「統計学的に導ける証拠」が「実験における証拠」になっている
- (E, x) と Ev(E, x) は区別される
- (E, x)
- パラメータ空間Ωについての記述
- Eの可能な結果xのサンプル空間についての記述
- Ev(E, x):実験的証拠
- どう評価するか?
- (E, x)
- (E, x) と Ev(E, x) は区別される
- 解明のポイント
- 2つの統計的証拠(E, x) と (E', y) が関係するあらゆる点で等しいと言える条件?
- 統計的証拠(E, x) と (E', y) が関係するあらゆる重要な点で等しい時、 Ev(E, x) = Ev(E', y)
- 2つの統計的証拠(E, x) と (E', y) が関係するあらゆる点で等しいと言える条件?
- 「統計学的に導ける証拠」が「実験における証拠」になっている
- 尤度原理からの重要な帰結
- サンプルスペース(可能だが実際には得られなかった確率変数の値)の無関係性
- 重要な争点
- 反事実の重要性を否定
- サンプルスペース(可能だが実際には得られなかった確率変数の値)の無関係性
対ベイズ主義
- デフィネッティ
- 確率、賭け、信念の関係
- 「合理的な賭けが成立するための条件」「確率の3つの規則」同じ条件
- D.ギリース「確率の哲学理論」
- 確率、賭け、信念の関係
- サヴェッジ
- Inductive inference と Inductive behavior
- 後者がより重要
- Inference
- 意見を変えること
- Behavior
- 分布と最終的な行為の経済的事実を用いて最も期待効用の高いものを選ぶ
- Inference
- 主観的 vs 客観的
- 信念変化の合理性
- 基礎付け主義
- 客観的事前確率
- ジェフリーズの無情報事前分布、ジェインズの最大エントロピー
- 哲学的ベイズ主義
- 実用への転換
尤度主義とは
- グレムリン仮説
- 哲学ではしばしば「説明可能性」と「確率」が結びつく
- 尤度主義の限界
- 尤度もモデルに依存するため恣意性が混じるが、なぜ尤度主義者はベイズ主義を批判できるのか?
- ミスリーディング確率というものを用いることで客観性を保証できる、というのがソーバーの立場
- ソーバーのAICの法則、どれぐらい使われているのか?
- あまり

