glmnetをもう少し理解したい①
久しぶりの更新です(いつも言っています)。
背景
データサイエンス入門シリーズの「スパース回帰分析とパターン認識」を読んでいたら大変面白かったので、いつものように glmnet の中身を見てみることにしました。
なお私は業務でLasso/Ridgeを使った経験があまりないため理解が間違っているかもしれませんが、その点あらかじめご了承ください。
こちらの本です。良い本です。
glmnet の実行結果
前回の GAM の時と同様に、まずは glmnet でどのような結果を得ることができるのか確認してみましょう。「スパース回帰分析とパターン認識」(以下、教科書)P12 コード1.2を(少し改変して)実行してみます。
なおこれらのコードはこちらからダウンロードすることもできます。
環境は以下のような感じです。
> sessionInfo() R version 3.6.0 (2019-04-26) Platform: x86_64-apple-darwin15.6.0 (64-bit) Running under: macOS Mojave 10.14.6 Matrix products: default BLAS: /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib locale: [1] ja_JP.UTF-8/ja_JP.UTF-8/ja_JP.UTF-8/C/ja_JP.UTF-8/ja_JP.UTF-8 attached base packages: [1] stats graphics grDevices utils datasets methods base loaded via a namespace (and not attached): [1] compiler_3.6.0 tools_3.6.0 grid_3.6.0 lattice_0.20-38
library(glmnet) library(plotmo) x <- scale(LifeCycleSavings[, 2:5]) y <- LifeCycleSavings[, 1] - mean(LifeCycleSavings[, 1]) lasso <- glmnet(x, y, family = "gaussian", alpha = 1) # alpha = 1 で lasso ridge <- glmnet(x, y, family = "gaussian", alpha = 0) # alpha = 0 で ridge ## directoryは適当に指定 png("./Image/glmnet_dive_01_01.png", width = 600, height = 400) plot_glmnet(lasso, xvar = "lambda", label = TRUE) dev.off() png("./Image/glmnet_dive_01_02.png", width = 600, height = 400) plot_glmnet(ridge, xvar = "lambda", label = TRUE) dev.off()
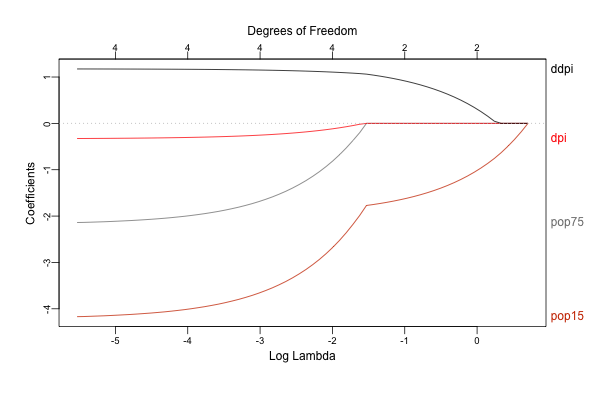
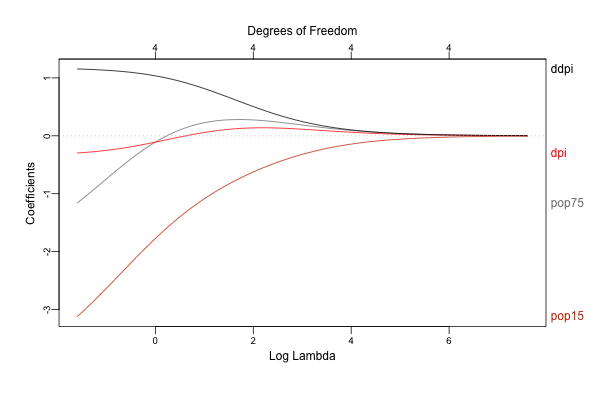
結果の解釈などについて詳しくは教科書を見て頂くとして、 glmnet は目的関数に回帰係数の規模に応じた罰則を設けることで、回帰係数を0に向かって縮小させながらフィッティングを行います。
またグラフのように罰則の大きさを色々と動かすことで各変数への回帰係数がどのように変化するかを評価することができます。
このグラフでは左から右に向かって罰則が強くなりますが、それにつれてLasso/Ridgeの両方とも回帰係数が0に向かって小さくなっている(縮小している)ことがわかります。
なお Lasso では回帰係数が0に収束している一方、 Ridge では微小ながら最後まで係数が0とならずに残っていることがわかりますが(グラフ上部の Degrees of Freedom が 4 のままとなっています)、 Lasso のように一部の回帰係数を正確に 0 と推定することが可能な手法をスパース推定と呼びます。
glmnet の実装
それでは glmnet という関数がどのように実装されているのか見ていきましょう。
まずはいつものように全体を眺め、見通しをよくします。
function (x, y, family = c("gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian"), weights, offset = NULL, alpha = 1, nlambda = 100, lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04), lambda = NULL, standardize = TRUE, intercept = TRUE, thresh = 1e-07, dfmax = nvars + 1, pmax = min(dfmax * 2 + 20, nvars), exclude, penalty.factor = rep(1, nvars), lower.limits = -Inf, upper.limits = Inf, maxit = 1e+05, type.gaussian = ifelse(nvars < 500, "covariance", "naive"), type.logistic = c("Newton", "modified.Newton"), standardize.response = FALSE, type.multinomial = c("ungrouped", "grouped"), relax = FALSE, trace.it = 0, ...) { ### 1. パラメータの設定、前処理、エラーチェック family = match.arg(family) if (alpha > 1) { warning("alpha >1; set to 1") alpha = 1 } if (alpha < 0) { warning("alpha<0; set to 0") alpha = 0 } alpha = as.double(alpha) this.call = match.call() nlam = as.integer(nlambda) y = drop(y) np = dim(x) if (is.null(np) | (np[2] <= 1)) stop("x should be a matrix with 2 or more columns") nobs = as.integer(np[1]) if (missing(weights)) weights = rep(1, nobs) else if (length(weights) != nobs) stop(paste("number of elements in weights (", length(weights), ") not equal to the number of rows of x (", nobs, ")", sep = "")) nvars = as.integer(np[2]) dimy = dim(y) nrowy = ifelse(is.null(dimy), length(y), dimy[1]) if (nrowy != nobs) stop(paste("number of observations in y (", nrowy, ") not equal to the number of rows of x (", nobs, ")", sep = "")) vnames = colnames(x) if (is.null(vnames)) vnames = paste("V", seq(nvars), sep = "") ne = as.integer(dfmax) nx = as.integer(pmax) if (missing(exclude)) exclude = integer(0) if (any(penalty.factor == Inf)) { exclude = c(exclude, seq(nvars)[penalty.factor == Inf]) exclude = sort(unique(exclude)) } if (length(exclude) > 0) { jd = match(exclude, seq(nvars), 0) if (!all(jd > 0)) stop("Some excluded variables out of range") penalty.factor[jd] = 1 jd = as.integer(c(length(jd), jd)) } else jd = as.integer(0) vp = as.double(penalty.factor) internal.parms = glmnet.control() if (internal.parms$itrace) trace.it = 1 else { if (trace.it) { glmnet.control(itrace = 1) on.exit(glmnet.control(itrace = 0)) } } if (any(lower.limits > 0)) { stop("Lower limits should be non-positive") } if (any(upper.limits < 0)) { stop("Upper limits should be non-negative") } lower.limits[lower.limits == -Inf] = -internal.parms$big upper.limits[upper.limits == Inf] = internal.parms$big if (length(lower.limits) < nvars) { if (length(lower.limits) == 1) lower.limits = rep(lower.limits, nvars) else stop("Require length 1 or nvars lower.limits") } else lower.limits = lower.limits[seq(nvars)] if (length(upper.limits) < nvars) { if (length(upper.limits) == 1) upper.limits = rep(upper.limits, nvars) else stop("Require length 1 or nvars upper.limits") } else upper.limits = upper.limits[seq(nvars)] cl = rbind(lower.limits, upper.limits) if (any(cl == 0)) { fdev = glmnet.control()$fdev if (fdev != 0) { glmnet.control(fdev = 0) on.exit(glmnet.control(fdev = fdev)) } } storage.mode(cl) = "double" isd = as.integer(standardize) intr = as.integer(intercept) if (!missing(intercept) && family == "cox") warning("Cox model has no intercept") jsd = as.integer(standardize.response) thresh = as.double(thresh) if (is.null(lambda)) { if (lambda.min.ratio >= 1) stop("lambda.min.ratio should be less than 1") flmin = as.double(lambda.min.ratio) ulam = double(1) } else { flmin = as.double(1) if (any(lambda < 0)) stop("lambdas should be non-negative") ulam = as.double(rev(sort(lambda))) nlam = as.integer(length(lambda)) } is.sparse = FALSE ix = jx = NULL if (inherits(x, "sparseMatrix")) { is.sparse = TRUE x = as(x, "CsparseMatrix") x = as(x, "dgCMatrix") ix = as.integer(x@p + 1) jx = as.integer(x@i + 1) x = as.double(x@x) } if (trace.it) { if (relax) cat("Training Fit\n") pb <- createPB(min = 0, max = nlam, initial = 0, style = 3) } kopt = switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) if (family == "multinomial") { type.multinomial = match.arg(type.multinomial) if (type.multinomial == "grouped") kopt = 2 } kopt = as.integer(kopt) ### 2. フィッティング fit = switch(family, gaussian = elnet(x, is.sparse, ix, jx, y, weights, offset, type.gaussian, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), poisson = fishnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), binomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), multinomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), cox = coxnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, vnames, maxit), mgaussian = mrelnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, jsd, intr, vnames, maxit)) if (trace.it) { utils::setTxtProgressBar(pb, nlam) close(pb) } ### 3. 後処理 if (is.null(lambda)) fit$lambda = fix.lam(fit$lambda) fit$call = this.call fit$nobs = nobs class(fit) = c(class(fit), "glmnet") if (relax) relax.glmnet(fit, x = x, y = y, weights = weights, offset = offset, lower.limits = lower.limits, upper.limits = upper.limits, check.args = FALSE, ...) else fit }
glmnet では以上のように、
- パラメータの設定、前処理、エラーチェック
- フィッティング
- 後処理
といったステップで処理が進んでおり、これは過去にみてきた glm や gam と同様ですね。
それでは各ステップを細かく見ていきましょう。
1. パラメータの設定、前処理、エラーチェック
まずはパラメータの設定や前処理に関わる部分ですが、はじめに family の指定が問題ないかをチェックします。
## 指定したfamilyが引数としてOKかチェック family = match.arg(family)
glmnet で使用可能な family は glm とは異なっており、Gamma / inverse.gaussian / quasi- が使えない代わりに、 multinomial / cox / mgaussian が使えるようになっています。
ここで multinomial は多項分布、mgaussian は多変量正規分布を意味するようです。
family のチェックには match.arg 関数が使われています。
この関数の挙動を理解するのは少し難しいのですが、こちらのブログが参考になります。
続いて alpha をチェックします:
## alpha ### LassoとRidgeそれぞれに対するペナルティの配分を決めるパラメータ ### glmnetにおける罰則項は以下で定義 ### alphaは0~1で、1ならLasso、0ならRidgeに対応 if (alpha > 1) { warning("alpha >1; set to 1") alpha = 1 } if (alpha < 0) { warning("alpha<0; set to 0") alpha = 0 } alpha = as.double(alpha)
glmnet においてこの alpha は、回帰係数のL1およびL2ノルムそれぞれに対する罰則の割合をコントロールします。
より具体的には、 glmnet では罰則項は以下によって定義されます(https://cran.r-project.org/web/packages/glmnet/glmnet.pdf の P19より):
冒頭のコードでは alpha = 1 または alpha = 0 としましたが、上の式から alpha = 1 のときにL2ノルムに対する罰則が消えてL1ノルムのみが残り(Lasso)、逆に alpha = 0 とするとL1ノルムに対する罰則が消えてL2ノルムが残る(Ridge)ことがわかります。
また alpha を (0, 1) とすると両者がそれぞれの割合でブレンドされます。
なお、ここでL2ノルムに対する罰則が1/2になっている理由はよくわかりませんでした。
glmnet の help で引用されているこちらの論文ではすでに $(1-\alpha)1/2||\beta||^2_2$ として定義されています。
またscikit-learnでも同様にL2ノルムに対しては0.5を乗じているようです(https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html)。
誰か理由を教えてください。
続いて match.call() を用いて引数の指定を正式なものに直します:
## match.call this.call = match.call()
これだけだと何を言っているかちょっとわからないと思いますので、以下の例で確認してみましょう:
myfun <- function(abc, def, ghi) { return(abc + 2*def + 3*ghi) }
上のように引数として abc 、 def 、 ghi を取る関数を定義します。
このとき R では、引数の指定がない場合には順番通りに入力されます:
> myfun(1, 2, 3) [1] 14
一部の引数のみ指定がある場合では指定された引数だけがその通りに入力され、残りは順番通りに割り当てられるようです。
> myfun(def = 3, 4, 5) [1] 25
ところでこの引数の指定は、一意に決まれば指定は省略することができます:
> myfun(d = 3, 4, 5) [1] 25
一方、例えば以下のような呼び出しでは g から始まる引数が2つあるため一意に決まらず、エラーとなってしまいます。
> myfun2 <- function(abc, def, ghi, gjk) { + return(abc + 2*def + 3*ghi + 4*gjk) + } > myfun2(g = 3, 4, 5, 6) myfun2(g = 3, 4, 5, 6) でエラー: 引数 1 が複数の仮引数に一致します
では match.call を使って関数を呼び出すとどうなるかと言うと:
> match.call(myfun, call("myfun", 1, def = 3, ghi = 5)) myfun(abc = 1, def = 3, ghi = 5)
この通り、各引数に対して何を割り当てたかを得ることができます。 便利ですね。
さらに続いて、 nlambda の指定です。
ここでは $\lambda$ (罰則の大きさ)そのものではなく、検証する $\lambda$ の数(nubmer of lambda)を指定します(デフォルトは100)。
## nlambda nlam = as.integer(nlambda)
ここからは y 、 x および weight のチェックです:
## drop y = drop(y) ## x ### x は2列以上持つ必要があるので、単回帰はできない様子 np = dim(x) if (is.null(np) | (np[2] <= 1)) stop("x should be a matrix with 2 or more columns") ### x のレコード数 nobs = as.integer(np[1]) ### weights ### 未入力のときは 1 を与え、weights と nobs が一致しないときはエラー if (missing(weights)) weights = rep(1, nobs) else if (length(weights) != nobs) stop(paste("number of elements in weights (", length(weights), ") not equal to the number of rows of x (", nobs, ")", sep = "")) ### 変数の数 nvars = as.integer(np[2]) ## y dimy = dim(y) ### y のレコード数 nrowy = ifelse(is.null(dimy), length(y), dimy[1]) ### y と x でレコード数が合わないときはエラー if (nrowy != nobs) stop(paste("number of observations in y (", nrowy, ") not equal to the number of rows of x (", nobs, ")", sep = "")) ## 変数名 vnames = colnames(x) if (is.null(vnames)) vnames = paste("V", seq(nvars), sep = "")
y に対する drop ですが、これは length が 1 であるような冗長な次元を落とす関数です。
続いて x の行数が weight や y と合わない場合にエラーを返しています。
以下ではモデルに含める変数や非ゼロとする変数などを指定します
( nx(=pmax) の方はちょっと理解がアヤシイので help の説明を書いておきます):
## 自由度 ### モデルに含まれる変数の上限を指定 ### dfmax = nvars + 1 ne = as.integer(dfmax) ### 非ゼロとする変数の数の上限(?) ### Limit the maximum number of variables ever to be nonzero ### pmax = min(dfmax * 2 + 20, nvars) nx = as.integer(pmax) ### 除外対象となる変数の指定 if (missing(exclude)) exclude = integer(0)
次に変数ごとに異なるペナルティを与えるために penalty.factor を指定します。
この数値が lambda に乗じられるため、例えば特定の変数に対して penalty.factor = 0 としておけば罰則を与えないようにすることが可能となります(結果として常にモデルに採用されるようになる):
## 変数ごとに異なるペナルティを与える ### デフォルトは 1 が入る ### Inf が指定されている変数は exclude として扱われる if (any(penalty.factor == Inf)) { exclude = c(exclude, seq(nvars)[penalty.factor == Inf]) exclude = sort(unique(exclude)) } if (length(exclude) > 0) { jd = match(exclude, seq(nvars), 0) if (!all(jd > 0)) stop("Some excluded variables out of range") penalty.factor[jd] = 1 jd = as.integer(c(length(jd), jd)) } else jd = as.integer(0) vp = as.double(penalty.factor)
これはせっかくなので実際にやってみましょう。
冒頭のコードを持ってきて、以下のように lambda を適当に設定してみます。
x <- scale(LifeCycleSavings[, 2:5]) y <- LifeCycleSavings[, 1] - mean(LifeCycleSavings[, 1])
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3)) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 1.182354e-15 pop15 -1.691002e+00 pop75 . dpi . ddpi 9.816514e-01
このとき、2・3番目の変数である pop75 と dpi は 0 と推定されてしまいました。
ここでこれらの変数の penalty.factor を 0 とすると
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3, + penalty.factor = c(1, 0, 0, 1))) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 9.523943e-16 pop15 -7.827680e-01 pop75 8.127991e-01 dpi -1.560908e-01 ddpi 6.812498e-01
ちゃんと推定されるようになっています。
逆に pop15 の penalty.factor を大きくすると
> coef(glmnet(x, y, family = "gaussian", alpha = 1, lambda = 0.3, + penalty.factor = c(2, 0, 0, 1))) 5 x 1 sparse Matrix of class "dgCMatrix" s0 (Intercept) 7.266786e-16 pop15 . pop75 1.374655e+00 dpi 2.586151e-02 ddpi 9.300500e-01
このようにモデルから除外されることになります。
さらに penalty.factor = Inf とすると、その変数は exclude として扱われるようになります。
続いて glmnet.control で持っているパラメータを渡します。
## 内部でデフォルトで持っているパラメータ internal.parms = glmnet.control() ### プログレスバーを表示する! if (internal.parms$itrace) trace.it = 1 else { if (trace.it) { glmnet.control(itrace = 1) on.exit(glmnet.control(itrace = 0)) } }
次に、回帰係数に対する上限・下限を設定します。 なお下限は non-positive 、上限は non-negative しか設定できないようですね。
## 上限・下限 ### lower.limit としては非正の値のみ指定できる if (any(lower.limits > 0)) { stop("Lower limits should be non-positive") } ### upper.limtit は逆に非負の値のみ指定できる if (any(upper.limits < 0)) { stop("Upper limits should be non-negative") } ### Inf (デフォルト)になっているものについては特定の値(9.9e35)に差し替え lower.limits[lower.limits == -Inf] = -internal.parms$big upper.limits[upper.limits == Inf] = internal.parms$big ### nvars との整合性チェック if (length(lower.limits) < nvars) { ### lower.limits としてスカラが指定されている場合は nvars 全てに適用 if (length(lower.limits) == 1) lower.limits = rep(lower.limits, nvars) else stop("Require length 1 or nvars lower.limits") } ### lower.limits が nvars よりも長い場合は前から利用する else lower.limits = lower.limits[seq(nvars)] ### nvars との整合性チェック(lower.limits と同様) if (length(upper.limits) < nvars) { if (length(upper.limits) == 1) upper.limits = rep(upper.limits, nvars) else stop("Require length 1 or nvars upper.limits") } else upper.limits = upper.limits[seq(nvars)] ### 上限・下限 ### coefficient limit? cl = rbind(lower.limits, upper.limits) ### lower または upper に 0 を含む場合 ### 0除算が発生するときのエラー対策? if (any(cl == 0)) { ### fdev は最小となるデビアンスの変化量(割合) ### minimum fractional change in deviance for stopping path; factory default = 1.0e5 fdev = glmnet.control()$fdev if (fdev != 0) { glmnet.control(fdev = 0) on.exit(glmnet.control(fdev = fdev)) # 関数終了時に実行される処理 } } storage.mode(cl) = "double"
標準化と切片に対する指定です。 標準化の処理そのものは以降の関数の内部で実行されるため、ここでは指定のみを行います。
## 標準化 ### standardize と intercept はデフォルトは TRUE なので 1 になる isd = as.integer(standardize) intr = as.integer(intercept) ### Cox回帰における警告 if (!missing(intercept) && family == "cox") warning("Cox model has no intercept") ### standardize.response は family="mgaussian" のときに目的変数を標準化するかの指定 jsd = as.integer(standardize.response)
収束を判定する閾値を指定します。
## 収束判定 ### coordinate descent における収束の閾値 thresh = as.double(thresh)
次に、 lambda に関する指定となりますが、 flmin および ulam の使われ方がよく理解できなかったため、これらの説明は省略します。
なお help にもありますが、通常は lambda には単一の値ではなく、候補となる値のベクトルを与えます。
Avoid supplying a single value for lambda (for predictions after CV use predict() instead).
## lambda ### ペナルティの大きさ ### 指定がない場合、flmin と ulam は lambda.min.ratio および 1 に指定される ### lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04) if (is.null(lambda)) { if (lambda.min.ratio >= 1) stop("lambda.min.ratio should be less than 1") flmin = as.double(lambda.min.ratio) ulam = double(1) } ### 指定がある場合、flmin(下限?)とulam(上限?)は 1 および lambdaの降順 に指定される else { flmin = as.double(1) if (any(lambda < 0)) stop("lambdas should be non-negative") ulam = as.double(rev(sort(lambda))) nlam = as.integer(length(lambda)) }
次に疎行列の指定です。
入力 X が疎行列である場合、dgCMatrix 形式に変換されます。
ここで dgCMatrix とは列方向の志向性を持つ疎行列の形式です。
## sparse matrix ### x が Matrix::sparseMatrix の場合は Matrix::dgCMatrix に変換する ### dgCMatrix: csc順に並び替えて(csc形式)の疎行列圧縮保管 is.sparse = FALSE ix = jx = NULL if (inherits(x, "sparseMatrix")) { is.sparse = TRUE x = as(x, "CsparseMatrix") x = as(x, "dgCMatrix") ### x@p は各列の非ゼロの値の個数を積み上げたものが格納されている(列数 + 1) ### diff(x@p + 1) すれば各列の非ゼロの値の個数がわかる ix = as.integer(x@p + 1) ### x@i は各列の非ゼロの値の行番号が格納されている(なので length(x@i) が非ゼロの値の個数と一致する) ### 0-index なので R のスタイルと合わせるために +1 しているのでしょう jx = as.integer(x@i + 1) ### x@x は非ゼロである値そのもののベクトル x = as.double(x@x) }
ここも、せっかくなので疎行列における数値の格納方法についても見ておきましょう。 以下のように疎行列を作成します:
set.seed(1234) i <- c(1, 5, 18) j <- c(4, 13, 19) n <- rnorm(3) m <- matrix(0, 20, 20) for (k in 1:length(n)) { m[i[k], j[k]] <- n[k] } s_m <- as(m, "dgCMatrix")
ここで s_m は行列 m を疎行列として扱ったものです。
str() で確認すると、 s_m には
@ i:非ゼロの要素の入っていた行番号( 0-index であることに注意)@ p:各列における非ゼロの要素の個数を積み上げたもの@ Dim:行列の次元@ Dimnames:行列の各次元の名前@ x:非ゼロの要素の数値@ factors:(これはちょっとわかりませんでした)
が格納されています。
> str(s_m) Formal class 'dgCMatrix' [package "Matrix"] with 6 slots ..@ i : int [1:3] 0 4 17 ..@ p : int [1:21] 0 0 0 0 1 1 1 1 1 1 ... ..@ Dim : int [1:2] 20 20 ..@ Dimnames:List of 2 .. ..$ : NULL .. ..$ : NULL ..@ x : num [1:3] -1.207 0.277 1.084 ..@ factors : list()
ここで @ i には非ゼロである各要素の行番号が入るため行列 m を作ったときの行番号の指定 i に対応しますが、0-index であるため数字は1つずつ小さくなっています。
> print(i- 1) [1] 0 4 17 > print(s_m@i) [1] 0 4 17
ちょっとわかりにくいのが @ p で、ここには各列における非ゼロの要素の個数の累積が格納され、列数に対応します(ただし最初に 0 が追加されるため、列数 + 1 の長さになります)。
今回の例では行列の列数が 20 なので、length が 21 となります。
> length(s_m@p) [1] 21
このベクトルには非ゼロの要素の個数の累積が入っているため、差分を取ると元の行列で非ゼロの要素が入っていた列を得ることができます。
> diff(s_m@p) [1] 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0
列番号を指定した j と比較してみましょう:
> which(diff(s_m@p) == 1) [1] 4 13 19 > j [1] 4 13 19
合っていますね。
続く処理では、 ix には各列における非ゼロの要素の累積個数(+1)を
、 jx には行番号を代入しています。
また x には元の疎行列における非ゼロの要素の値そのものをベクトルとして入力しており、説明変数の行列が疎行列であった場合、この時点で行列ではなくベクトルとして扱われることになります。
次に、プログレスバーの指定です(出せるんですね)。
## プログレスバー if (trace.it) { if (relax) cat("Training Fit\n") pb <- createPB(min = 0, max = nlam, initial = 0, style = 3) }
そして最後に最適化の手法についての指定です。
family が `binomial または multinomial の場合、 glmnet の引数である type.logistic および type.multinomial が評価され、(後の工程で)それに応じて呼ばれる関数が変わります。
具体的には lognet2m 、 lognetn および multlognetn のどれが選ばれるかが決まります。
これは別の機会に解説します(予定です)。
## 最適化の手法(ロジスティックおよび多項ロジスティックの時) ### type.logistic = c("Newton", "modified.Newton") ### Newton を指定なら 0、modified.Newton を指定なら 1 を返す ### If "Newton" then the exact hessian is used (default), while "modified.Newton" uses an upper-bound on the hessian, and can be faster. kopt = switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) ### type.multinomial = c("ungrouped", "grouped") ### 多項ロジスティックで更にgroupedの場合は kopt は 2 となる ### If "grouped" then a grouped lasso penalty is used on the multinomial coefficients for a variable. This ensures they are all in our out together. ### The default is "ungrouped" if (family == "multinomial") { type.multinomial = match.arg(type.multinomial) if (type.multinomial == "grouped") kopt = 2 } kopt = as.integer(kopt)
最初の方で family のチェックに使われ、ここでも使われている match.arg ですが、せっかくなので挙動を確認しておきましょう:
### 引数に type.logistic を持つ関数を定義 myfun <- function(a = "aaa", type.logistic = c("Newton", "modified.Newton")) { ### 呼び出し元の関数の引数をチェックし、 Newton なら 0、modified.Newton なら 1を割り当てる kopt <- switch(match.arg(type.logistic), Newton = 0, modified.Newton = 1) kopt }
上のような関数を定義し、以下のように呼び出すと、結果はそれぞれ 0, 0, 1 となります。
> myfun() [1] 0 > myfun(type.logistic = "Newton") [1] 0 > myfun(type.logistic = "modified.Newton") [1] 1
2. フィッティング
以上でパラメータの設定や前処理が終わりましたので次はフィッティングです。
といってもここでは family に応じて呼び出す関数を変えているだけなので、詳細は一旦スキップしましょう。
# フィッティング ## family に応じてその後に呼び出す関数を変える fit = switch(family, ### gaussian のときは elnet gaussian = elnet(x, is.sparse, ix, jx, y, weights, offset, type.gaussian, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), ### poisson のときは fishnet poisson = fishnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit), ### binomial のときは lognet binomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), ### multinomial のときも lognet multinomial = lognet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, intr, vnames, maxit, kopt, family), ### cox のときは coxnet cox = coxnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, vnames, maxit), ### mgaussian のときは mrelnet mgaussian = mrelnet(x, is.sparse, ix, jx, y, weights, offset, alpha, nobs, nvars, jd, vp, cl, ne, nx, nlam, flmin, ulam, thresh, isd, jsd, intr, vnames, maxit)) ## プログレスバー if (trace.it) { utils::setTxtProgressBar(pb, nlam) close(pb) }
なおここでそれぞれの関数に渡されている引数を比較すると以下のようになります(一部はよくわかりませんでした):
| 引数 | 説明 | elnet | fishnet | lognet | coxnet | mrelnet |
|---|---|---|---|---|---|---|
| x | 説明変数の行列 | 〇 | 〇 | 〇 | 〇 | 〇 |
| is.sparse | 疎行列であるかの指定 | 〇 | 〇 | 〇 | 〇 | 〇 |
| ix | 疎行列における非ゼロの要素の累積個数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jx | 疎行列における非ゼロの要素の行番号 | 〇 | 〇 | 〇 | 〇 | 〇 |
| y | 目的変数の行列 | 〇 | 〇 | 〇 | 〇 | 〇 |
| weights | 観測値に対する重み | 〇 | 〇 | 〇 | 〇 | 〇 |
| offset | オフセット | 〇 | 〇 | 〇 | 〇 | 〇 |
| type.gaussian | 1:covariance, 2:naïve | 〇 | - | - | - | - |
| alpha | L1とL2に対する重みの調整パラメータ | 〇 | 〇 | 〇 | 〇 | 〇 |
| nobs | レコード数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| nvars | 説明変数の数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jd | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| vp | 各変数に対する罰則の重み(penalty.factor) | 〇 | 〇 | 〇 | 〇 | 〇 |
| cl | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| ne | モデルに含まれる変数の上限。ne = dfmax = nvars + 1 | 〇 | 〇 | 〇 | 〇 | 〇 |
| nx | 非ゼロとする変数の個数の上限? | 〇 | 〇 | 〇 | 〇 | 〇 |
| nlam | lambdaの数 | 〇 | 〇 | 〇 | 〇 | 〇 |
| flmin | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| ulam | ? | 〇 | 〇 | 〇 | 〇 | 〇 |
| thresh | 収束判定の閾値 | 〇 | 〇 | 〇 | 〇 | 〇 |
| isd | standardizeするかの指定 | 〇 | 〇 | 〇 | 〇 | 〇 |
| jsd | ? | - | - | - | - | 〇 |
| intr | 切片(Intercept)を含めるかの指定 | 〇 | 〇 | 〇 | - | 〇 |
| vnames | 変数名 | 〇 | 〇 | 〇 | 〇 | 〇 |
| maxit | 反復回数の上限 | 〇 | 〇 | 〇 | 〇 | 〇 |
| kopt | 最適化の手法 | - | - | 〇 | - | - |
| family | family | - | - | 〇 | - | - |
3. 後処理
最後に後処理です。
# 後処理 ## lambda が指定されておらず fit$lambda が 3 パターン以上検証されている場合、先頭を差し替える ## glmnet::fix.lam ## function (lam) { ## if (length(lam) > 2) { ## llam = log(lam) ## lam[1] = exp(2 * llam[2] - llam[3]) ## } ## lam ## } if (is.null(lambda)) fit$lambda = fix.lam(fit$lambda) ## call fit$call = this.call ## レコード数 fit$nobs = nobs ## class に glmnet を追加 class(fit) = c(class(fit), "glmnet") # リターン ## relax が TRUE の場合、解パスの各セットについて罰則なしでモデルをフィッティングする ## If TRUE then for each active set in the path of solutions, the model is refit without any regularization. See details for more information. ## This argument is new, and users may experience convergence issues with small datasets, especially with non-gaussian families. ## Limiting the value of ’maxp’ can alleviate these issues in some cases. if (relax) relax.glmnet(fit, x = x, y = y, weights = weights, offset = offset, lower.limits = lower.limits, upper.limits = upper.limits, check.args = FALSE, ...) else fit
この後処理で目立つ工程としては relax の部分でしょう。
ここで relax は help によると、
If relax=TRUE a duplicate sequence of models is produced, where each active set in the elastic-net path is refit without regularization. The result of this is a matching "glmnet" object which is stored on the original object in a component named "relaxed", and is part of the glmnet output.
ということで、glmnet によって変数選択された結果を用いて、罰則なしで再度フィッティングを行うオプションのようです。
これも実際にやってみるのが早いと思いますので、以下のように実行してみます:
lasso_02 <- glmnet(x, y, family = "gaussian", relax = T)
すると、先程の結果( lasso )に、 lasso_02$relaxed という結果が追加されていることがわかりますが、内容は lasso とほとんど同じです。
> str(lasso) List of 12 $ a0 : Named num [1:68] 6.11e-16 6.71e-16 7.26e-16 7.76e-16 8.22e-16 ... ..- attr(*, "names")= chr [1:68] "s0" "s1" "s2" "s3" ... $ beta :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots .. ..@ i : int [1:216] 0 0 0 0 0 3 0 3 0 3 ... .. ..@ p : int [1:69] 0 0 1 2 3 4 6 8 10 12 ... .. ..@ Dim : int [1:2] 4 68 .. ..@ Dimnames:List of 2 .. .. ..$ : chr [1:4] "pop15" "pop75" "dpi" "ddpi" .. .. ..$ : chr [1:68] "s0" "s1" "s2" "s3" ... .. ..@ x : num [1:216] -0.181 -0.347 -0.497 -0.634 -0.757 ... .. ..@ factors : list() $ df : int [1:68] 0 1 1 1 1 2 2 2 2 2 ... $ dim : int [1:2] 4 68 $ lambda : num [1:68] 2.02 1.84 1.68 1.53 1.39 ... $ dev.ratio: num [1:68] 0 0.0352 0.0645 0.0888 0.1089 ... $ nulldev : num 984 $ npasses : int 562 $ jerr : int 0 $ offset : logi FALSE $ call : language glmnet(x = x, y = y, family = "gaussian", alpha = 1) $ nobs : int 50 - attr(*, "class")= chr [1:2] "elnet" "glmnet" > str(lasso_02$relaxed) List of 12 $ a0 : Named num [1:68] 6.11e-16 1.29e-15 1.29e-15 1.29e-15 1.29e-15 ... ..- attr(*, "names")= chr [1:68] "s0" "s1" "s2" "s3" ... $ beta :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots .. ..@ i : int [1:216] 0 0 0 0 0 3 0 3 0 3 ... .. ..@ p : int [1:69] 0 0 1 2 3 4 6 8 10 12 ... .. ..@ Dim : int [1:2] 4 68 .. ..@ Dimnames:List of 2 .. .. ..$ : chr [1:4] "pop15" "pop75" "dpi" "ddpi" .. .. ..$ : chr [1:68] "s0" "s1" "s2" "s3" ... .. ..@ x : num [1:216] -2.04 -2.04 -2.04 -2.04 -1.98 ... .. ..@ factors : list() $ df : int [1:68] 0 1 1 1 1 2 2 2 2 2 ... $ dim : int [1:2] 4 68 $ lambda : num [1:68] 2.02 1.84 1.68 1.53 1.39 ... $ dev.ratio: num [1:68] 0 0.208 0.208 0.208 0.208 ... $ nulldev : num 984 $ npasses : int 562 $ jerr : int 0 $ offset : logi FALSE $ call : language glmnet(x = x, y = y, family = "gaussian", relax = T) $ nobs : int 50 - attr(*, "class")= chr [1:2] "elnet" "glmnet"
ここで lasso_02$relaxed の中身を少し見てみると、例えば beta には以下のような数値が入っています。
> lasso_02$relaxed$beta[, 1:6] 4 x 6 sparse Matrix of class "dgCMatrix" s0 s1 s2 s3 s4 s5 pop15 . -2.040996 -2.040996 -2.040996 -2.040996 -1.980216 pop75 . . . . . . dpi . . . . . . ddpi . . . . . 1.270865
これは何かと言うと、少しずつ罰則の重みを変えたことで変数が選択された状態で通常の線形回帰を当てはめたときの回帰係数となっています。
例えば lasso_02$relaxed$beta[, 6] には、変数として選択された pop15 と ddpi それぞれの回帰係数が入っています。
実際に lm の結果と一致するか見てみましょう:
> coef(lm(y ~ x[, c(1, 4)])) (Intercept) x[, c(1, 4)]pop15 x[, c(1, 4)]ddpi 1.364331e-15 -1.980216e+00 1.270865e+00
合っていますね。
ところで切片の推定値が入っている lasso_02$relaxed$a0 の値は少し異なるようです:
> lasso_02$relaxed$a0[6] s5 1.28119e-15
なんでやろか。。
もしかしたら標準化の違いかとも思いましたがそれでもないようで、この理由はわかりませんでした。
lasso_03 <- glmnet(x, y, family = "gaussian", relax = T, standardize = F)
> lasso_03$relaxed$a0[6] s5 1.28119e-15
glmnet() の実装は以上となります。
次回はフィッティングの部分で呼ばれている elnet を詳しく見ていきましょう。
なお gam のときとは違い、 glmnet では library をインストールしてもソースコードは付いてきませんでしたので、こちらを参考に fortran のソースコードを取得しました。
ではまた次回。
