階層ベイズと状態空間モデルで広告効果を推定したい
背景
これまでMarketing Mix Modeling(MMM)におけるAdStock効果の推定について色々と記事を書いてきましたが、その他にも試したいと思っているモデルがいくつかあります。その一つが階層ベイズモデルと状態空間モデルを同時に取り扱うものです。
例えば「地域別の売上推移のデータ」が手元にあると考えてみましょう。地域ではなく人や商品でも構いませんが、ある要因の各水準がそれぞれ時系列データを持っている状況(いわゆるパネルデータ)で、ひとまずここでは地域とします。このようなデータはあらゆる会社で保有していることでしょう。 今、各地域についてMMMにより広告効果を推定することを考えたとき、どのようなモデリングが可能でしょうか?
シンプルに考えれば、地域ごとに一つずつモデルを作るという方法が挙げられます。例えば地域の数が2つ3つしかなかったり、モデルの作成に時間をかけることが可能であればこの方法は有効かもしれません。しかし問題もあります。地域ごとに独立してモデルを作成するということは、各地域のパラメータは互いに独立であるとの仮定を置くことになるのですが、それは事実でしょうか?
確かにTVや新聞には地方欄やローカル局があり、地域限定のコンテンツや提供される場合もあるでしょう。しかしどちらかと言えば全国で同じコンテンツが提供される割合の方が大きいでしょうし、購買行動に地域による差がそれほど認められるとは、経験的にも思えません。もし仮に地域による異質性というものがそれほど強くないのであれば、むしろそういった情報を積極的に活かした方が良いのではないでしょうか?
目的
そのような時に、パラメータ間に緩やかな縛りをかける方法として階層ベイズモデルという手法があります。詳しくは書籍1を参考にして頂くとして、ここでは「各地域の広告効果を表すパラメータを生成する分布を仮定する」方法と説明しておきます。この分布の幅(バラつき、分散)が十分に大きければ広告効果は地域によって様々な値を取り得ますし、逆に分布の幅が極端に狭ければ地域ごとの広告効果に差はないことを意味します。
この階層構造を持つモデルを、時系列データの分析でお馴染みの状態空間モデルと合わせて取り扱いたいというのが今回の試みです。具体的には、以下のようなモデルを想定しています。
添字のAおよびtはそれぞれ地域(Area)と時点(time)を意味しており、は「ある地域
Aのt時点における観測値」となります。
ポイントは4行目で、地域ごとの広告効果に対して、その生成元となる分布(ここでは正規分布)を仮定しています。もし
が大きければ
は様々な値を取り得ますが、値が小さければ非常に似通った値になることが理解できると思います。
ライブラリの読み込み
今回の分析では{rstan}を使用します。階層ベイズ + 状態空間モデルといった非常に複雑なモデルを表現できるのが強みです。
library(tidyverse) library(ggplot2) library(rstan) options(mc.cores = parallel::detectCores()) rstan_options(auto_write = TRUE)
シミュレーションデータの生成
分析用のデータを生成しますが、検証のポイントとしては以下のようになります:
- 5地域(
num_region)から4年分(num_year)の月次(num_month)データを収集し、合計240点の観測値を得たと想定 - 回帰係数(広告効果)は平均
0.5、分散0.01の正規分布にしたがって発生 - 状態変数のパラメータは各地域で共通
## シードの固定 set.seed(123) ## 観測値の数 num_region <- 5 num_month <- 12 num_year <- 4 data_length <- num_month * num_year ## 回帰係数 mu_beta <- 0.5 var_beta <- 0.01 beta_ad <- rnorm(num_region, mu_beta, sqrt(var_beta)) beta_ad_all <- rep(beta_ad, each = data_length) ## 分布の設定 # 状態変数の初期値 state_t0 <- 3 var_state_t0 <- 1 # 状態変数の分散 var_state <- 0.01 # 誤差項 var_error <- 0.01 ## 説明変数X scale_x <- 5 zero_per <- 0.2 X <- ifelse(runif(num_region * data_length) > zero_per, 1, 0) * rpois(num_region * data_length, scale_x)
上記の条件に従いデータを発生させます。状態変数を除けば先に示したモデルの通り簡単な線形モデルです。Area_IDは、後ほどStanでフィッティングを行うために必要となる変数で、YMは描画用です。
## 状態変数 State <- matrix(0, nrow = num_region * data_length) for (i in 1:num_region) { for (j in 1:data_length) { if (j == 1) { ## 1, 49, 97, 145, 193行目が各地域の先頭となる State[(i-1) * data_length + j] <- rnorm(1, state_t0, sqrt(var_state_t0)) } else { State[(i-1) * data_length + j] <- State[(i-1) * data_length + j - 1] + rnorm(1, 0, sqrt(var_state)) } } } ## 目的変数 error <- rnorm(num_region * data_length, 0, sqrt(var_error)) Y <- State + X * beta_ad_all + error ## 地域ごとのID Area_ID <- 1:num_region DF <- data.frame( "Area_ID" = rep(Area_ID, each = data_length), "YM" = rep(1:data_length, time = num_region), "Y" = Y, "X" = X, "True_s" = State, "True_e" = error)
ここで観測値と状態変数が各地域でどのように推移しているか確認しておきます。
DF %>% gather("Var", "Val", -c(Area_ID, YM)) %>% filter(Var %in% c("Y", "True_s")) %>% ggplot(., aes(x = YM, y = Val, color = Var)) + geom_line() + facet_wrap(~Area_ID)
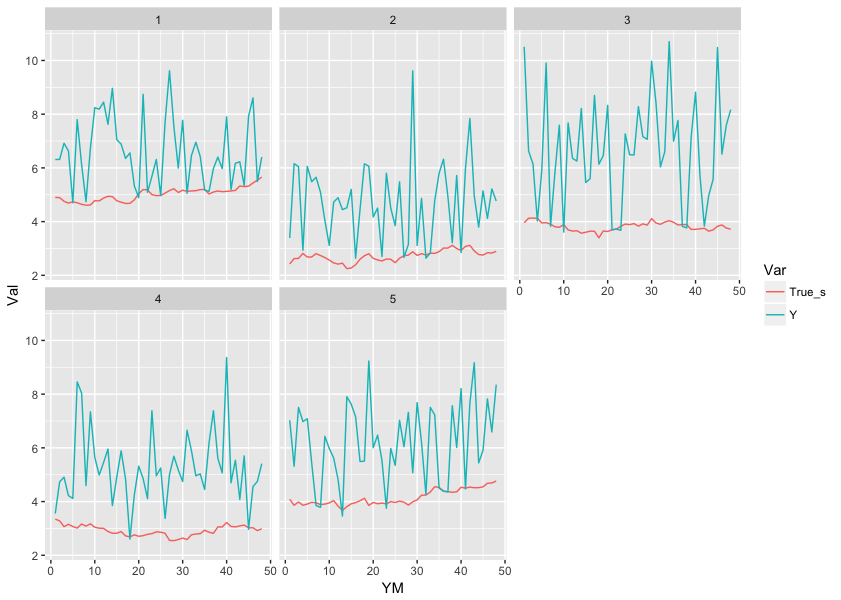
また、この時点で地域をまとめてlmで推定した$\beta$がどのようになるかも確認しておきましょう。
> coef(lm(Y ~ X, data = DF)) (Intercept) X 3.8088184 0.5003114
また地域ごとにデータを分割した場合も試してみます。
results <- list() for (i in Area_ID) { results[[as.character(i)]] <- coef(lm(Y ~ X, data = DF, subset = Area_ID == i)) }
> print(cbind(do.call("rbind", results), beta_ad)) (Intercept) X beta_ad 1 5.066906 0.4292258 0.4439524 2 2.700195 0.4837768 0.4769823 3 3.764447 0.6628493 0.6558708 4 2.953617 0.4988667 0.5070508 5 4.051693 0.5314325 0.5129288
そこそこ近い値が推定されていますね(汗
Stanによるフィッティング
気を取り直して、Stanを用いたフィッティングを実行してみます。Stanに渡すデータは以下の通りです。
dat_Stan <- list(N = data_length, K = num_region, Y = DF$Y, X = DF$X, Area_ID = DF$Area_ID)
またStanのスクリプトは以下のようになります。
data { int N; // 地域ごとの観測値の数(data_length) int K; // 地域の数(num_region) vector[N*K] Y; // 観測値のベクトル vector[N*K] X; // 説明変数のベクトル int<lower=1, upper=K> Area_ID[N*K]; } parameters { real state_t0; // 状態変数の0期目の平均 vector[N*K] state; // 状態変数のベクトル real beta_0; // 回帰係数の事前分布の平均 vector[K] beta; // 地域ごとの回帰係数のベクトル real<lower=0> var_state_t0; // 状態変数の0期目の分散 real<lower=0> var_state; // 状態変数の分散 real<lower=0> var_beta_0; // 回帰係数の事前分布の分散 real<lower=0> var_error; // 誤差分散 } model { // 状態変数をサンプリング for (k in 1:K) { // 1期目の値は0期目の分布からサンプルする state[1 + (k-1)*N] ~ normal(state_t0, var_state_t0); // 2期目以降は前期の値を平均とした分布からサンプルする for(i in 2:N) { state[i + (k-1)*N] ~ normal(state[i-1 + (k-1)*N], var_state); } } // 回帰係数をサンプリング for (k in 1:K) { beta[k] ~ normal(beta_0, var_beta_0); } // Yをサンプリング for(i in 1:(N*K)) { Y[i] ~ normal(state[i] + beta[Area_ID[i]] * X[i], var_error); } }
このスクリプトをHB_SSM_Sim.stanとして保存し、フィッティングを行います。
fit_01 <- stan(file = '/YourDirectory/HB_SSM_Sim.stan', data = dat_Stan, iter = 1000, chains = 4, seed = 123)
結果の確認
フィッティングが終わったので、結果を見てみましょう。fit_01からサンプルを抽出して加工します。
## サンプルを抽出する res_01 <- rstan::extract(fit_01) ## 該当するパラメータを取り出す ests <- summary(fit_01)$summary t0_rows <- rownames(ests)[grep("state_t0", rownames(ests))] state_rows <- rownames(ests)[grep("state\\[", rownames(ests))] b0_rows <- rownames(ests)[grep("beta_0", rownames(ests))] beta_rows <- rownames(ests)[grep("beta\\[", rownames(ests))] ## 状態変数 state_par <- ests %>% data.frame %>% select(mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% state_rows) %>% mutate("Area" = DF$Area_ID) state_cmp <- data.frame( True = State, Est = state_par$mean, Area = as.factor(state_par$Area), YM = DF$YM )
まずは状態変数の推定結果を見てみましょう。実際の値と推定値を並べてみます。 (なお以降の作業の前にサンプルのtraceプロットとヒストグラムを確認し、収束していると判断しています)
state_cmp %>% gather("Var", "Val", -c(Area, YM)) %>% ggplot(., aes(x = YM, y = Val, colour = Var)) + geom_line() + facet_wrap(~Area)
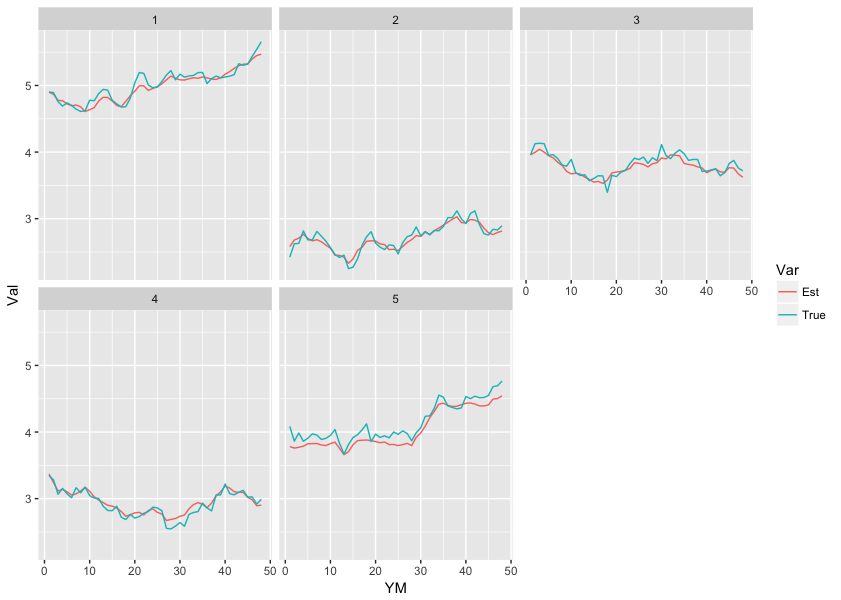
おぉ、かなり精度良く推定できているようですね!状態変数の初期値や分散の推定値はどうでしょうか?
> ests %>% data.frame %>% select(mean) %>% rename("Estimated" = mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% t0_rows) %>% mutate("True" = c(state_t0, var_state_t0)) %>% mutate("Simulated" = c( mean(DF[c(1, 49, 97, 145, 193), "True_s"]), var(DF[c(1, 49, 97, 145, 193), "True_s"]) )) %>% select(Par, True, Simulated, Estimated) Par True Simulated Estimated 1 state_t0 3 3.7429556 3.731479 2 var_state_t0 1 0.8521877 1.328192
状態変数初期値の平均および分散の真の値がそれぞれ3および1であったのに対し、生成されたデータでは3.7および0.85でした。推定された値は3.7および1.3で、分散がやや過大に推定されているようです。ただし以下に示すように、推定値の95%信用区間も結構広いため、逸脱しているとまでは言えないようです。
> ests %>% data.frame %>% select(X2.5., X97.5.) %>% rename("Lower95" = X2.5., "Upeer95" = X97.5.) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% t0_rows) %>% select(Par, everything()) Par Lower95 Upeer95 1 state_t0 2.3975622 5.027106 2 var_state_t0 0.5549254 3.525860
続いて回帰係数はどうでしょうか。
beta_par <- ests %>% data.frame %>% select(mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% beta_rows) beta_cmp <- data.frame( True = beta_ad, Est = beta_par$mean ) ggplot(beta_cmp, aes(x = True, y = Est)) + geom_point() + coord_fixed()
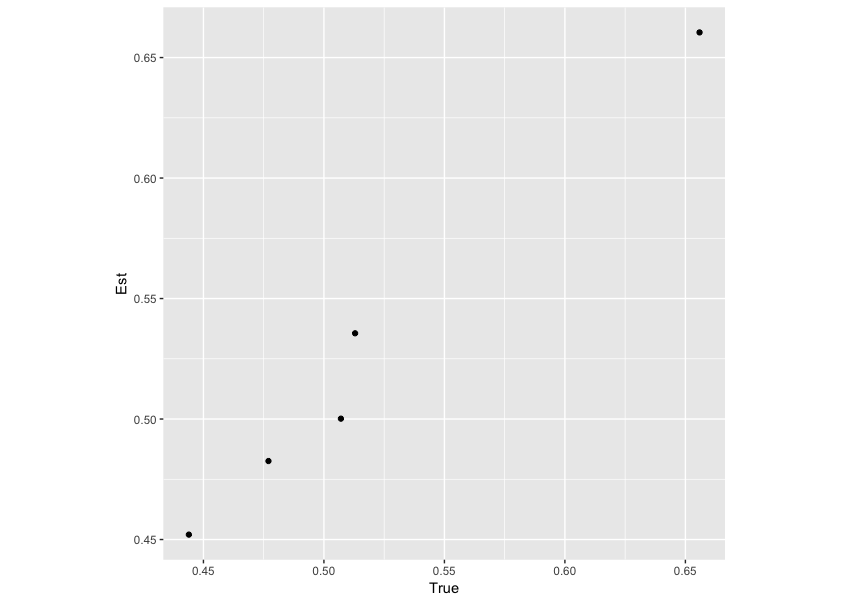
こちらも、事前に設定した回帰係数と推定値が似通っているようです。数値を確認しても、良い精度で推定できています。
ests %>% data.frame %>% select(mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% beta_rows) %>% bind_cols("True" = beta_ad) %>% select(Par, True, mean) Par True mean 1 beta[1] 0.4439524 0.4520343 2 beta[2] 0.4769823 0.4825661 3 beta[3] 0.6558708 0.6604340 4 beta[4] 0.5070508 0.5001494 5 beta[5] 0.5129288 0.5355829
最後に、回帰係数の事前分布についても見ておきましょう。
> ests %>% data.frame %>% select(mean) %>% mutate("Par" = rownames(ests)) %>% filter(Par %in% b0_rows) %>% bind_cols("True" = c(mu_beta, var_beta)) %>% select(Par, True, mean) Par True mean 1 beta_0 0.50 0.5184981 2 var_beta_0 0.01 0.1385978
回帰係数の事前分布の分散はちょっと大きく推定されているようですが、平均は近しい値となっているようです。
終わりに
以上、「階層ベイズと状態空間モデルを合わせて取り扱いたい」という試みでしたが、結果としては概ね満足の行くものになったと思います。序盤に書いた通り、階層ベイズ + 状態空間モデルのような非常に複雑なモデルであっても、stanを使えば非常に簡単に推定が可能です。
これまで広告効果の推定に関していくつか記事を書いてきましたが、実はゴールとなるモデルとしてはこれを想定していました。あとはこのモデルに、これまで紹介してきたようなAdStock効果の推定を組み込めば試してみたかったモデルは一通り完了することになります。
これらについても追って紹介したいと思います。