GLMをもう少し理解したい③
前回の記事において、GLMでは以下の方程式を用いてパラメータベクトルを推定するという話をしました:
今回はその続きです。
※ 1/25 記事を修正しました
最尤推定
上の式には情報行列の逆行列が入っているので、前から情報行列を乗じます:
ところで、(ここもまた天下りですが)スコアは以下の式で表されますが*1、
はスコア
の分散共分散行列であり、上記の式から
となり、さらにから以下のようになります:
これを行列で表記すると:
となります。ただしは
となる対角行列です。よって冒頭の式(1)の左辺はと書けます。
次に右辺ですが、式(2)から以下のように書けます:
このとき1項目と2項目をでくくり、残りを
とすると
が得られます。これは線形モデルに対する重み付き最小二乗法を適用して得られる正規方程式と同じ形となりますが、や
は
に依存するため、反復的に解く必要があります。
なおでくくる際、
を使っているため二項目にはこの逆数である
が残り、
にはそれが渡ります。すなわち:
です。
※ 以下のセクションでと
の関係を取り違えて説明していたので修正しました
さて、このに含まれる
はどのような形になるでしょうか?GLMにおいて
は
線形予測子線形予測子で説明されるもので、をリンク関数で変換したもの
はそれを逆リンク関数で変換したものでした。つまり、
という関係であることを思い出すと、は分析者が事前に設定したリンク関数に依存することになります。例えばリンク関数としてlogを指定していれば、
となります。identityなら1になるでしょう。
同様にに含まれる
は、
が
であることから逆リンク関数に依存します。例えば逆リンク関数がexpなら
となるでしょう。
以上から、、
、
が分かれば
を更新することができ、またそれぞれについても具体的に計算できそうです。GLMではこの反復重み付き最小二乗法(IRLS, Iteratively Reweighted Least Squares)によって最尤推定量を求めます。
それでは次回は、具体的な数値を使って計算してみましょう。
*1:Dobsonの式(4.18)より。この式の導出がちょっと煩雑だったので割愛。
GLMをもう少し理解したい②
前回の記事からだいぶ間が空いてしまいましたが続きを書いてみます。なおこの記事は主にDobsonの「一般化線形モデル入門」の第3・4章を参考にしていますので、そちらも合わせてご確認ください。良書です。

- 作者: Annette J.Dobson,田中豊,森川敏彦,山中竹春,冨田誠
- 出版社/メーカー: 共立出版
- 発売日: 2008/09/08
- メディア: 単行本
- 購入: 15人 クリック: 152回
- この商品を含むブログ (13件) を見る
さて、前回の記事では、以下のように結びました:
つまり
glmは最尤法によって解を推定していると思われている(そしてそれは正しい)のだけれど、実際には最小二乗解をHouseholder法によって得ているのだということがわかりました。
これは果たしてどういうことなのでしょうか?これについて答えるために以下の流れで見ていきます。
※1/22 記事を少し修正しました
ニュートン・ラプソン法
初めにニュートン・ラプソン法についてです。やや天下り的で申し訳ないのですが、一般にGLMでは解を推定する際に数値的な解法を必要とします(理由については後述します追記:考えていた説明が誤っていたので削除します)。その際に用いられる手法としてニュートン・ラプソン法というものがあり、これは非線形な方程式の解を反復によって求める手法です。
あまり詳しい説明はできませんが、原理的には以下の式を反復的に更新することで求めたい解を得ることができます:
ここでおよび
はそれぞれ更新前後の解となります。
は対象となる関数、
はその導関数を表します。以下の例で簡単に見てみましょう:
x <- seq(-3, 3, 0.1) y <- sin(x) plot(x, y, type = "l")

上記のようなsin関数においてとなる点を見つけます。先ほど示したニュートン・ラプソンのアルゴリズムに従い、
- 初期値を入力
- 関数およびその導関数による返り値を計算する
- 解を更新する
- 更新後の関数値が十分0に近くなったら反復を停止する
ことで最終的な解を得ます。Rで書くと以下のようになるでしょう:
iteration <- 0 # イテレータ threshold <- 1e-02 # 反復の停止を判断する閾値 x_old <- -1 # 更新前の解 updates <- 1 # 更新後の解による関数値(の絶対値) while (updates > threshold) { x_new <- x_old - sin(x_old)/cos(x_old) # 更新後の解を得る updates <- abs(sin(x_new)) # 更新後の解による関数値を得る x_old <- x_new # 解を更新する cat(sprintf("Iterations: %i, X_New: %f \n", iteration, x_new)) # 表示 iteration <- iteration + 1 # イテレータを増やす }
上記のスクリプトを実行すると下のような結果が得られました。
Iterations: 1, X_New: 0.557408 Iterations: 2, X_New: -0.065936 Iterations: 3, X_New: 0.000096
3回の反復でほぼに収束している様子がわかります。この例の場合は
において
つまり
が0となることが示されました1。
スコア法
上記では一般的なニュートン・ラプソン法の原理を紹介しましたが、本記事のテーマであるGLMに置き換えると、および
はそれぞれ
および
が対象となります。ここで
はパラメータ、即ち推定したい対象であり、
は対数尤度関数の導関数です。
なぜ対数尤度関数そのものではなく対数尤度関数の導関数なのでしょうか?これについては以下のような図を考えるとわかりやすいかもしれません。
x <- seq(-2, 3, 0.1) quad <- function(x) -(x-1)^2 + 3 derive <- function(x) -2 * x + 2 plot(x, quad(x), type = "l", ylim = c(-10, 10), ylab = "") par(new = T) plot(x, derive(x), type = "l", col = "red", ylim = c(-10, 10), ylab = "f(x) or f'(x)") lines(x, rep(0, length(x)), lty = 2, col = "blue")

ここで黒い線は対象となる関数(二次関数)、赤い線はその導関数、青い点線はy = 0を示しています。
先ほどニュートン・ラプソン法の節において
となる点を見つけます
と書きましたが、このアルゴリズムでは返り値が0となる点を見つける一方、我々が得たいのは対数尤度関数を最大にする点です。このグラフで言えば黒い線を最大にするようなです。
もしこの黒い線に対してニュートン・ラプソン法を当てはめるとどうなるでしょうか?おそらく黒い線と青い線が交わるところに収束するでしょう。先ほどのスクリプトを少し修正してみます:
iteration <- 0 threshold <- 1e-02 x_old <- 0 # 初期値を変更 updates <- 1 while (updates > threshold) { x_new <- x_old - quad(x_old)/derive(x_old) # 関数を変更 updates <- abs(quad(x_new)) x_old <- x_new iteration <- iteration + 1 cat(sprintf("Iterations: %i, X_New: %f \n", iteration, x_new)) }
Iterations: 1, X_New: -1.000000 Iterations: 2, X_New: -0.750000 Iterations: 3, X_New: -0.732143
-0.732143という点で収束しましたが、quad(-0.732143)は-0.0003193724となるため、確かにが0となる点を見つけているようです。しかしこれは最大となる値ではありません。
それでは赤い線で試してみるとどうでしょうか?答えはグラフからも明らかですが、元々の目的である黒い線の最大値で収束しそうです。
上記のような理由により、GLMにニュートン・ラプソンを当てはめる場合には、対数尤度関数そのものではなく対数尤度関数の導関数を用いると言えそうです。
それでは改めて、GLMにおけるニュートン・ラプソン法の推定方程式を見てみましょう:
ここでは対数尤度関数を
で微分したもので、スコア関数、スコア統計量、または単にスコアなどと呼ばれます。
はスコアを更に微分したものとなりますが、最尤推定においては
そのものではなく
により近似したものを用いることがあります。このとき、
という関係があるため2、先程の方程式は以下のように書き直されます:
さらに推定対象をパラメータのベクトルに置き換えると:
と一般化され、この式を用いて解を得る方法をスコア法と言います。
最尤推定
それでは上の式がそれぞれどのように得られるのかを確認していきますが、ここで一度切りたいと思います。
小話
以下は全て憶測に依るもので、全く根拠のない話です。
ハイパフォーマーを発見するための分析を考えたとき、過去の個人ごとの業績から予測モデルを構築すると、「性別」の効果が有意に効くのではと思います1。そしてそれはきっと、男性の効果がプラス(または女性だとマイナス)になるでしょう。
もちろんこれは、業績に対して男女に差があることを示すものというよりも、他の条件が同一であったとしても女性の業績が低く評価されやすい現象(いわゆるガラスの天井)を、「性別」という効果が吸収してしまっているだけなんだと思います。しかし、そのようにして構築したモデルをテストデータ(つまりは新入社員)に対して当てはめると、潜在的な能力に係わらず、女性は不当に低く評価されてしまいます。
これを避けるにはどうしたら良いかと言うと、答えは簡単で、予測の際には「性別」の効果を予測モデルから外せば良いだけです。ここでのポイントは、モデルを学習する際にはガラスの天井効果を調整するために「性別」の効果を入れつつも、予測の際にはそれを用いないという点にあります。
このような操作が可能なところが線形モデル(GLMやGAMを含む)の良いところだと思うのですが、しかし同時に、その解釈可能性の高さ故に誤解を招くこともあるんじゃないかとも思います。つまり、学習した結果を見た人が短絡的に「女性の方が能力が低い」と理解してしまうことを助長してしまうのではないでしょうか。
その可能性を考えると、むしろ解釈可能性が低いアルゴリズムの方が良いのかもしれません。そのようなアルゴリズムでは、線形モデルのように単純に性別の効果を外して予測を行うことができるわけではないでしょうけども、例えば全ての対象者について真の性別に係わらず一律に男性 or 女性としておけばガラスの天井効果が紛れることを避けられます。
そう考えると、今後の機械学習界隈において「解釈可能性の高いモデル」は本当に求められるべきものなのか悩みます。
-
性別は単に例として挙げただけで、ここは学歴でも出身地方でも人種でも何でも構いません。↩
GLMをもう少し理解したい①
背景
一般化線形モデル(GLM)は、一般に線形回帰モデルを正規分布を含む指数分布族に拡張したものだと捉えられています。アイディアとしてはシンプルである割に非常に有用で、GLMによって
- 整数値(ポアソン回帰)
- 二値(ロジスティック回帰)
0〜1の実数(ベータ回帰)※2020/4/8追記 ベータ回帰は一般的でなかったので消しておきます- 0以上の実数(ガンマ回帰) ※2020/4/8追記 代わりにガンマ回帰を追加
などを扱うことができ、しかも回帰係数という非常に解釈性の高い結果を得ることができます1。
そんなGLMですが、よく使う割には内容を今ひとつ理解できていないなと思うことがあったので、もう少しだけGLMを理解したいと思いRのglmの中身を見てみました。その内容をメモしておきます。
ちなみにこの検証を行っている環境は以下の通りです:
> sessionInfo() R version 3.3.3 (2017-03-06) Platform: x86_64-apple-darwin13.4.0 (64-bit) Running under: macOS 10.13.3 locale: [1] ja_JP.UTF-8/ja_JP.UTF-8/ja_JP.UTF-8/C/ja_JP.UTF-8/ja_JP.UTF-8 attached base packages: [1] stats graphics grDevices utils datasets methods base loaded via a namespace (and not attached): [1] tools_3.3.3 yaml_2.1.13 knitr_1.15.1
glm
まずはRのglmがどのように定義されているかを見てみましょう。コンソールでglmと入力することで、以下のようにglmという関数の定義を見ることができます。
> glm function (formula, family = gaussian, data, weights, subset, na.action, start = NULL, etastart, mustart, offset, control = list(...), model = TRUE, method = "glm.fit", x = FALSE, y = TRUE, contrasts = NULL, ...)
まずはここでglmに渡す引数を定義しています。これらの引数でよく使われるのはformula、family、dataでしょうか。それぞれglmに渡す線形予測子(数式)、Yの従う分布、モデリングに用いるデータを指定しています。その他、データポイントの一つ一つの重みを変えたい場合にはweights、データの一部を使用する場合にはsubsetを指定したりします。
関数の定義は以下より始まりますが、細かい話は飛ばしてglmの本体に向かいましょう。
{ call <- match.call() if (is.character(family)) family <- get(family, mode = "function", envir = parent.frame()) ## ## 中略 ## ## 本体はココのようです fit <- eval(call(if(is.function(method)) "method" else method, x = X, y = Y, weights = weights, start = start, etastart = etastart, mustart = mustart, offset = offset, family = family, control = control, intercept = attr(mt, "intercept") > 0L))
glmの本体と呼べそうな部分はどうやらこのfitを定義している部分です。最初のevalは与えられた文字列をスクリプトとして解釈するための関数なので、call以降を実行するようです。またcallはここによると「与えられた名前の関数の、与えられた引数への適応からなる未評価の表現式である」とのことなので、callに続くmethodおよび残りの引数がmethod(...)の形でevalに与えられ、関数として評価されます。
つまり
eval(call(if(is.function(method)) "method" else method, ...
は
method(...)
と同じとなるはずで、以下の例では同じように動いていることが確認できました。
# 関数を定義 return_cube <- function(x) x^3 # 普通に呼び出す > return_cube(3) [1] 27 # eval(call(...))で呼び出す > eval(call("return_cube", x = 3)) [1] 27 # match.call > eval(match.call(return_cube, call("return_cube", x = 3))) [1] 27 > eval(match.call(return_cube, call("return_cube", 3))) [1] 27
さて、callで指定しているmethodはglmの引数で指定されているものでしたが、デフォルトではglm.fitが入力されています。したがってmethod(...)はglm.fit(...)となるはずです。そこで今度はglm.fitの定義を確認してみましょう。
glm.fit
glmと同じく、glm.fitについてもコンソールに直接打ち込むことで関数の定義を表示することができます。まずは引数から見てみましょう。
> glm.fit function (x, y, weights = rep(1, nobs), start = NULL, etastart = NULL, mustart = NULL, offset = rep(0, nobs), family = gaussian(), control = list(), intercept = TRUE)
x、yはそれぞれ説明変数と目的変数を指定し、その他の引数はglmから引き継がれるようですね。
またメインとなるのは以下のループ部分のようです。
control <- do.call("glm.control", control) x <- as.matrix(x) xnames <- dimnames(x)[[2L]] ## ## 中略 ## for (iter in 1L:control$maxit) { ## ## 中略 ## z <- (eta - offset)[good] + (y - mu)[good]/mu.eta.val[good] w <- sqrt((weights[good] * mu.eta.val[good]^2)/variance(mu)[good]) fit <- .Call(C_Cdqrls, x[good, , drop = FALSE] * w, z * w, min(1e-07, control$epsilon/1000), check = FALSE) ## ## 中略 ## } ## ## 中略 ##
do.call(...)に渡すcontrolはlist()なので、do.call("glm.control", list())を実行すると以下が返ります;
> do.call("glm.control", list()) $epsilon [1] 1e-08 $maxit [1] 25 $trace [1] FALSE
maxitが25なので、このループは最大で25回実行されます。ではこのループ内で何が行われているかというと、zとwを新たに定義し、それをxおよび互いに乗じた形でC_Cdqrlsに渡しています。また.CallはCで書かれたルーチンを呼び出すための関数なので、ここではC_Cdqrlsという関数にx * wやz * wといった引数を渡しているようです。
ではこのC_Cdqrlsはどこにあるのでしょうか?今度はC_Cdqrlsを探してみましょう。
C_Cdqrls
実はこのC_Cdqrlsはstatsパッケージの関数として定義されています。しかしエクスポートされていないため、そのままコンソールに打ち込んでも表示されません。そのような場合には:::を使います。
> stats:::C_Cdqrls $name [1] "Cdqrls" $address <pointer: 0x101a2cdd0> attr(,"class") [1] "RegisteredNativeSymbol" $dll DLL name: stats Filename: /Library/Frameworks/R.framework/Versions/3.3/Resources/library/stats/libs/stats.so Dynamic lookup: FALSE $numParameters [1] 4 attr(,"class") [1] "CallRoutine" "NativeSymbolInfo"
しかしstats:::C_Cdqrlsと打ち込んでも、これまでと異なり関数の定義が表示されません。これは先ほど書いた通り、C_CdqrlsがCで書かれた関数であり、.callで呼び出されるためです。
ではどこから呼び出されるのかと言うと、私の環境では上記のFilenameで指定されている場所のようなのですが、これ自体は実行ファイル(stats.so)となっていてソースが見当たりません。それじゃどこにあるのかということで色々とググってみたところ、どうやらここで見れそうです。ファイル名を見てわかる通り、これはlmを定義しているコードです。glmは深く潜っていくとlmにたどり着くようです。
C_Cdqrlsを定義している部分を見てみると:
SEXP Cdqrls(SEXP x, SEXP y, SEXP tol, SEXP chk)
{
SEXP ans;
###
### 中略
###
work = (double *) R_alloc(2 * p, sizeof(double));
F77_CALL(dqrls)(REAL(qr), &n, &p, REAL(y), &ny, &rtol,
REAL(coefficients), REAL(residuals), REAL(effects),
&rank, INTEGER(pivot), REAL(qraux), work);
SET_VECTOR_ELT(ans, 4, ScalarInteger(rank));
for(int i = 0; i < p; i++)
if(ip[i] != i+1) { pivoted = 1; break; }
SET_VECTOR_ELT(ans, 8, ScalarLogical(pivoted));
UNPROTECT(nprotect);
return ans;
}
ここまで来ると何がなんだか私にはわかりませんが、returnでansを返しているのでansを定義している箇所に着目すると、どうもF77_CALLが怪しい感じです。F77_CALLはこのページによるとCからFortranを呼び出すための関数のようです。
F77_CALL
ではFortranで書かれたdqrlsのソースコードはどこで見れるのかと言うと、ここのようです。重要そうなところを抜き出すと:
subroutine dqrls(x,n,p,y,ny,tol,b,rsd,qty,k,jpvt,qraux,work) integer n,p,ny,k,jpvt(p) double precision x(n,p),y(n,ny),tol,b(p,ny),rsd(n,ny), . qty(n,ny),qraux(p),work(p) integer info,j,jj,kk ### Householder transformation call dqrdc2(x,n,n,p,tol,k,qraux,jpvt,work) ### if(k .gt. 0) then do 20 jj=1,ny call dqrsl(x,n,n,k,qraux,y(1,jj),rsd(1,jj),qty(1,jj), 1 b(1,jj),rsd(1,jj),rsd(1,jj),1110,info) 20 continue else do 35 i=1,n do 30 jj=1,ny rsd(i,jj) = y(i,jj) 30 continue 35 continue endif
となっており、dqrdc2とdqrsl(紛らわしいけどdqrlsではない)を呼んでいます。これらはそれぞれ、
- Householder変換を行う関数
- そのアウトプットに対して加工および最小二乗解を与える関数
となっています。
随分かかりましたが、ここに来てようやく解を得ることができました。ここまでを振り返ると、glmという関数のコアの部分の役割はそれぞれ:
- Householder法による最小二乗解の推定(
C_Cdqrls) - 上記の反復による収束判定(
glm.fit) - もろもろの条件設定など(
glm)
となっているようでした。つまりglmは最尤法によって解を推定していると思われている(そしてそれは正しい)のだけれど、実際には最小二乗解をHouseholder法によって得ているのだということがわかりました。
長くなってしまったので、一旦切ります。次回はこの意味についてもう少し追いかけてみたいと思います。
ロジスティック回帰の小ネタ
小ネタ①:ロジスティック回帰は集計値を用いても同じ結果となる
tmp <- epitools::expand.table(Titanic) library(tidyverse) dat_table <- tmp %>% group_by(Class, Sex, Age) %>% summarise("Yes" = sum(Survived == "Yes"), "No" = sum(Survived == "No"))
集計値
> summary(glm(cbind(Yes, No) ~ ., dat_table, family = binomial("logit")))$coef Estimate Std. Error z value Pr(>|z|) (Intercept) 0.6853195 0.2729943 2.510380 1.206013e-02 Class2nd -1.0180950 0.1959976 -5.194427 2.053519e-07 Class3rd -1.7777622 0.1715666 -10.361935 3.694112e-25 ClassCrew -0.8576762 0.1573389 -5.451138 5.004844e-08 SexFemale 2.4200603 0.1404101 17.235655 1.434207e-66 AgeAdult -1.0615424 0.2440257 -4.350125 1.360598e-05
生データ
> summary(glm(Survived ~ ., tmp, family = binomial("logit")))$coef Estimate Std. Error z value Pr(>|z|) (Intercept) 0.6853195 0.2729934 2.510388 1.205986e-02 Class2nd -1.0180950 0.1959969 -5.194443 2.053331e-07 Class3rd -1.7777622 0.1715657 -10.361993 3.691891e-25 ClassCrew -0.8576762 0.1573387 -5.451147 5.004592e-08 SexFemale 2.4200603 0.1404093 17.235750 1.431830e-66 AgeAdult -1.0615424 0.2440247 -4.350143 1.360490e-05
標準誤差がわずかに異なるものの、回帰係数は一致。
小ネタ②:ロジスティック回帰とロジットに対する線形回帰は異なる
set.seed(123) n <- 10000 x1 <- sample(c("A", "B"), n, replace = T) x1_A <- ifelse(x1 == "A", 1, 0) x1_B <- ifelse(x1 == "B", 1, 0) x2 <- sample(c("X", "Y", "Z"), n, replace = T) x2_X <- ifelse(x2 == "X", 1, 0) x2_Y <- ifelse(x2 == "Y", 1, 0) x2_Z <- ifelse(x2 == "Z", 1, 0) b0 <- 0 b1_B <- 1.0 b2_Y <- 1.5 b2_Z <- 3.0 l <- b0 + x1_B * b1_B + x2_Y * b2_Y + x2_Z * b2_Z p <- exp(l) / (1 + exp(l)) dat <- data.frame( y = rbinom(n, 1, p), x1 = x1, x2 = x2 ) tmp <- dat %>% group_by(x1, x2) %>% summarise("Yes" = sum(y == 1), "No" = sum(y == 0)) %>% mutate(p = Yes / (Yes + No)) %>% mutate(logit = log(p / (1-p)))
> summary(glm(y ~ x1 + x2, dat, family = binomial("logit")))$coef Estimate Std. Error z value Pr(>|z|) (Intercept) 0.003870327 0.04524904 0.0855339 9.318369e-01 x1B 1.005336861 0.05966550 16.8495494 1.057171e-63 x2Y 1.548350891 0.06500045 23.8206168 2.042443e-125 x2Z 3.016559809 0.10570629 28.5371830 4.051563e-179
> summary(lm(logit ~ x1 + x2, tmp))$coef Estimate Std. Error t value Pr(>|t|) (Intercept) -0.03945677 0.09246599 -0.4267166 0.711129289 x1B 1.08845178 0.09246599 11.7713743 0.007139621 x2Y 1.55366958 0.11324725 13.7192702 0.005271007 x2Z 3.08631608 0.11324725 27.2529016 0.001343688
回帰係数は概ね一致するものの標準誤差に大きな違いがあり、結果的にP値は大きく異なる。
RとPythonの結果を一致させたい
背景
通常、私はデータを分析する際には主にRを使用します。しかし分析結果を既存のシステムに投入するなど実装を考えた場合には、Rではなく別の言語を求められることもあると思います。 今回、RとPythonのそれぞれでGLMを実行したときに結果が一致するのかを検証する機会があったため、その内容を備忘がてら紹介しておきます。
RからPythonを呼び出す
今回の検証では、RからPythonを呼び出すためのライブラリreticulateを使用しました。RStudioからR Notebookとして使えば、chunkごとにRとPythonを切り替えることができて大変便利です。
なおMacユーザーでPython環境としてAnacondaをインストールしている場合、.Rprofileに以下を記載しておくことでAnaconda配下のPythonを呼び出すことができます。
Sys.setenv(PATH = paste("/anaconda3/bin", Sys.getenv("PATH"), sep=":"))
では早速reticulateをインストールし、Pythonを呼び出せるか試してみましょう。
install.packages("reticulate") library(reticulate)
> system("python --version") Python 3.6.4 :: Anaconda custom (64-bit)
このような表示が出れば成功です。
線形回帰
まずはじめに、irisのデータを用いて線形回帰をかけてみます。Rでは以下のように書くことができます。
> glm(Sepal.Length ~ Petal.Length, data = iris, family = gaussian) Call: glm(formula = Sepal.Length ~ Petal.Length, family = gaussian, data = iris) Coefficients: (Intercept) Petal.Length 4.3066 0.4089 Degrees of Freedom: 149 Total (i.e. Null); 148 Residual Null Deviance: 102.2 Residual Deviance: 24.53 AIC: 160
上記をPythonのstatsmodelsを使って同じように書いてみましょう。irisのデータは事前にRから書き出しておいたものを使用することとし、pandasのread_csvで読み込みます。そのデータをstatsmodelsのGLMに渡します。
import statsmodels.api as sm import pandas as pd iris = pd.read_csv("/YourDirectory/iris.csv") res_iris = sm.GLM(iris['Sepal.Length'], iris['Petal.Length'], family = sm.families.Gaussian()).fit() print(res_iris.summary()) Generalized Linear Model Regression Results ============================================================================== Dep. Variable: Sepal.Length No. Observations: 150 Model: GLM Df Residuals: 149 Model Family: Gaussian Df Model: 0 Link Function: identity Scale: 3.521367262403398 Method: IRLS Log-Likelihood: -306.75 Date: Mon, 04 Jun 2018 Deviance: 524.68 Time: 18:30:59 Pearson chi2: 525. No. Iterations: 2 ================================================================================ coef std err z P>|z| [0.025 0.975] -------------------------------------------------------------------------------- Petal.Length 1.3489 0.037 36.530 0.000 1.277 1.421 ================================================================================
ひとまず分析を実行することはできたようですが、Rの結果とは違いますね。出力されたテーブルの下部にある「coef」を見てみると、切片が出力されていません。statsmodelsはデフォルトでは切片が入らないようです。
statsmodelsで切片を追加するにはadd_constantを使います。以下のように修正しましょう。
import statsmodels.api as sm import pandas as pd iris = pd.read_csv("/YourDirectory/iris.csv") res_iris_2 = sm.GLM(iris['Sepal.Length'], sm.add_constant(iris['Petal.Length']), family = sm.families.Gaussian()).fit() print(res_iris_2.summary()) Generalized Linear Model Regression Results =============================================================================== Dep. Variable: Sepal.Length No. Observations: 150 Model: GLM Df Residuals: 148 Model Family: Gaussian Df Model: 1 Link Function: identity Scale: 0.16570968760697133 Method: IRLS Log-Likelihood: -77.020 Date: Thu, 31 May 2018 Deviance: 24.525 Time: 13:37:26 Pearson chi2: 24.5 No. Iterations: 2 ================================================================================ coef std err z P>|z| [0.025 0.975] -------------------------------------------------------------------------------- const 4.3066 0.078 54.939 0.000 4.153 4.460 Petal.Length 0.4089 0.019 21.646 0.000 0.372 0.446 ================================================================================
無事、Rの結果と一致しました。
ロジスティック回帰
続いてTitanicのデータを用いてロジスティック回帰をかけてみます。Titanicのデータは下記のコードによりdataframeに加工し、iris同様に書き出しておきました。
tmp <- data.frame(Titanic) titanic <- data.frame(Class = rep(tmp$Class, tmp$Freq), Sex = rep(tmp$Sex, tmp$Freq), Age = rep(tmp$Age, tmp$Freq), Survived = rep(tmp$Survived, tmp$Freq))
Rでは以下のように書けます。
> glm(Survived ~ ., data = titanic, family = binomial(link = "logit")) Call: glm(formula = Survived ~ ., family = binomial(link = "logit"), data = titanic) Coefficients: (Intercept) Class2nd Class3rd ClassCrew SexMale AgeChild 2.0438 -1.0181 -1.7778 -0.8577 -2.4201 1.0615 Degrees of Freedom: 2200 Total (i.e. Null); 2195 Residual Null Deviance: 2769 Residual Deviance: 2210 AIC: 2222
これをPythonで実行してみましょう。ここではRのformulaと同じように指定するためにstatsmodels.formula.apiを使用します。
import statsmodels.api as sm import statsmodels.formula.api as smf import pandas as pd import numpy as np dat = pd.read_csv("/YourDirectory/titanic.csv") dat = dat.drop('Unnamed: 0', axis = 1) titanic_formula = "Survived ~ Class + Sex + Age" glm_bin = smf.glm(formula = titanic_formula, data = dat, family = sm.families.Binomial(sm.families.links.logit)).fit() print(glm_bin.summary()) Generalized Linear Model Regression Results ============================================================================================= Dep. Variable: ['Survived[No]', 'Survived[Yes]'] No. Observations: 2201 Model: GLM Df Residuals: 2195 Model Family: Binomial Df Model: 5 Link Function: logit Scale: 1.0 Method: IRLS Log-Likelihood: -1105.0 Date: Mon, 04 Jun 2018 Deviance: 2210.1 Time: 16:58:29 Pearson chi2: 2.25e+03 No. Iterations: 5 ================================================================================= coef std err z P>|z| [0.025 0.975] --------------------------------------------------------------------------------- Intercept -2.0438 0.168 -12.171 0.000 -2.373 -1.715 Class[T.2nd] 1.0181 0.196 5.194 0.000 0.634 1.402 Class[T.3rd] 1.7778 0.172 10.362 0.000 1.441 2.114 Class[T.Crew] 0.8577 0.157 5.451 0.000 0.549 1.166 Sex[T.Male] 2.4201 0.140 17.236 0.000 2.145 2.695 Age[T.Child] -1.0615 0.244 -4.350 0.000 -1.540 -0.583 =================================================================================
やはり、結果が異なります。よく見ると、カテゴリカル変数についてRではFemaleとAdultが推定されているのに対して、PythonではMaleとChildが推定されていることがわかります。どうやら参照列(Reference)が異なるようです。
Rの方で、Referenceを変更して確認してみましょう。
titanic$Sex <- relevel(titanic$Sex, ref = "Female") titanic$Age <- relevel(titanic$Age, ref = "Adult") > glm(Survived ~ ., data = titanic, family = binomial(link = "logit")) Call: glm(formula = Survived ~ ., family = binomial(link = "logit"), data = titanic) Coefficients: (Intercept) Class2nd Class3rd ClassCrew SexMale AgeChild 2.0438 -1.0181 -1.7778 -0.8577 -2.4201 1.0615 Degrees of Freedom: 2200 Total (i.e. Null); 2195 Residual Null Deviance: 2769 Residual Deviance: 2210 AIC: 2222
これで結果が近くなりましたが、まだ一致していません。回帰係数の絶対値は同じとなりましたが符号が異なっています。目的変数であるYesとNoという文字列が、RとPythonで別々に解釈された可能性があります。
今度はPython側でYesとNoの定義を修正してみましょう。
import statsmodels.api as sm import statsmodels.formula.api as smf import pandas as pd import numpy as np dat = pd.read_csv("/YourDirectory/titanic.csv") dat = dat.drop('Unnamed: 0', axis = 1) dat['Survived'] = dat['Survived'].str.replace('No', '0') dat['Survived'] = dat['Survived'].str.replace('Yes', '1') dat['Survived'] = dat['Survived'].astype(np.int64) titanic_formula = "Survived ~ Class + Sex + Age" glm_bin_2 = smf.glm(formula = titanic_formula, data = dat, family=sm.families.Binomial(sm.families.links.logit)).fit() print(glm_bin_2.summary()) Generalized Linear Model Regression Results ============================================================================== Dep. Variable: Survived No. Observations: 2201 Model: GLM Df Residuals: 2195 Model Family: Binomial Df Model: 5 Link Function: logit Scale: 1.0 Method: IRLS Log-Likelihood: -1105.0 Date: Mon, 04 Jun 2018 Deviance: 2210.1 Time: 17:03:20 Pearson chi2: 2.25e+03 No. Iterations: 5 ================================================================================= coef std err z P>|z| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 2.0438 0.168 12.171 0.000 1.715 2.373 Class[T.2nd] -1.0181 0.196 -5.194 0.000 -1.402 -0.634 Class[T.3rd] -1.7778 0.172 -10.362 0.000 -2.114 -1.441 Class[T.Crew] -0.8577 0.157 -5.451 0.000 -1.166 -0.549 Sex[T.Male] -2.4201 0.140 -17.236 0.000 -2.695 -2.145 Age[T.Child] 1.0615 0.244 4.350 0.000 0.583 1.540 =================================================================================
これで一致しました。
終わりに
今回見てきたように、同一かつシンプルなモデルであっても、言語の仕様によって出力は容易に変わります。異なる結果が得られたときに大慌てしなくて済むよう、各言語や関数についての仕様を把握しておき、本当に異なる結果となっているのかをチェックするというのが大切です。特にモデルの結果を実システムに組み込む際にはエンジニアによるリファクタリングが行われることも多いでしょうから、エンジニアがハマりそうなポイントを押さえておくと役立ちそうですね。
Stanを使って変数選択したい
背景
Stanを使ってモデリングをしている時に不満を感じる点として、変数選択が難しいということが挙げられます。もともと私自身は、例えばStepwiseやLassoなどを用いた"機械的な"変数選択があまり好きではない1のですが、それでも分析を効率的に進める上でそれらの手法に頼りたくなることがあります。
そういったときにglmを用いているのであればstep関数により容易に変数選択が可能なのですが、Stanではそうもいきません。何か良い方法はないかと探していたところ、StanのGithubレポジトリに{projpred}というそれっぽいlibraryを見つけたので、紹介がてら変数の選択精度を実験してみます2。
データ準備
ライブラリの読み込み
今回の分析では{rstan}の代わりに{rstanarm}というlibraryを使用します。{rstanarm}はRのglmと同じようなシンタックスのままでモデルをベイズ化することが可能で、例えば{rstanarm}のvignetteでは以下のようなスニペットが紹介されています(一部改変あり)3。
library(rstanarm) data("womensrole", package = "HSAUR3") womensrole$total <- womensrole$agree + womensrole$disagree womensrole_bglm_1 <- stan_glm(cbind(agree, disagree) ~ education + gender, data = womensrole, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4, cores = 1, seed = 123)
> womensrole_bglm_1 stan_glm family: binomial [logit] formula: cbind(agree, disagree) ~ education + gender observations: 42 predictors: 3 ------ Median MAD_SD (Intercept) 2.5 0.2 education -0.3 0.0 genderFemale 0.0 0.1 Sample avg. posterior predictive distribution of y: Median MAD_SD mean_PPD 24.3 0.8 ------ For info on the priors used see help('prior_summary.stanreg').
数字の意味は一旦置いておきますが、今回はこちらのlibraryを使用しながら進めていきます。
続いて他のlibraryを読み込みます。この辺りはvignetteそのままです。
library(projpred) library(ggplot2) library(bayesplot) theme_set(theme_bw()) options(mc.cores = parallel::detectCores())
シミュレーションデータの作成
実験を進めるにあたりシミュレーションデータを作成します。もちろんlibraryに付属のデータセットを使っても良いのですが、そのまま同じことをするのも面白くないので以下のように複数のデータを作成して結果を比較してみましょう:
- 説明変数の数が少なく(20)、連続変数のみ
- 説明変数の数が多く(100)、連続変数のみ
- 説明変数の数が少なく(20)、ダミー変数を含む
- 説明変数の数が多く(100)、ダミー変数を含む
見てわかる通りで、説明変数の数とダミー変数の有無によって4パターンを用意します。なぜこのパターンにしたかというと、単純にvignetteを見ていて連続変数ばかりだなと思ったのと、サンプルデータの説明変数の数が20ぐらいで、これなら機械的な選択に頼らなくても自力でどうにかできそうだな、と思ったためです。
各パターンについて特にひねりもなくデータを作成します。なお真のモデルは1と2、3と4で同一のものとしました。したがって2と4の状況は、1と3それぞれに比べて「不要なデータのみが追加された状態」での変数選択という状況になります。
以下のように各パラメータを設定します。
set.seed(1) N <- 100 # number of observations xn_1 <- 20 # number of variables for pattern 1 xn_2 <- 100 # number of variables for pattern 2 b1 <- 0.5 # regression coefficient of X[, 1] b2 <- 0.8 # regression coefficient of X[, 2] var_e <- 1 # residual variance
パターン1 & 2について、まず乱数によりXを生成し、そのうちの2列を使ってYを作成します。またその2列を含む20列および全列を各パターンの説明変数とします。
X <- matrix(rnorm(N * xn_2, 0, 1), nrow = N, ncol = xn_2) Y <- 1.0 + X[, 1] * b1 + X[, 2] * b2 + rnorm(N, 0, var_e) X1 <- X[, 1:xn_1] X2 <- X[, 1:xn_2] dat1 <- data.frame("Y" = Y, "X" = I(X1)) dat2 <- data.frame("Y" = Y, "X" = I(X2))
データセットを作成する際にX1をI()で渡すことで、X1全体を"X"として再定義できます。すると以下のようなformulaが実行可能になります。
> lm(Y ~ X, dat1) Call: lm(formula = Y ~ X, data = dat1) Coefficients: (Intercept) X1 X2 X3 X4 X5 X6 1.038393 0.422365 0.824111 0.006940 -0.064897 0.060024 -0.004623 X7 X8 X9 X10 X11 X12 X13 -0.096471 0.040521 0.123807 -0.051311 0.125116 0.009435 0.014924 X14 X15 X16 X17 X18 X19 X20 0.065920 -0.037135 -0.110772 -0.015537 -0.003969 -0.136834 0.095512
もちろんそのまま渡して.で指定するのでも構いません。
tmp <- data.frame("Y" = Y, "X" = X1)
> lm(Y ~ ., tmp) Call: lm(formula = Y ~ ., data = tmp) Coefficients: (Intercept) X.1 X.2 X.3 X.4 X.5 X.6 1.038393 0.422365 0.824111 0.006940 -0.064897 0.060024 -0.004623 X.7 X.8 X.9 X.10 X.11 X.12 X.13 -0.096471 0.040521 0.123807 -0.051311 0.125116 0.009435 0.014924 X.14 X.15 X.16 X.17 X.18 X.19 X.20 0.065920 -0.037135 -0.110772 -0.015537 -0.003969 -0.136834 0.095512
続いてパターン3 & 4についても基本的に同じ流れでデータを作成しますが、一部にダミー変数を含めます。
Z <- matrix(rnorm(N * xn_2, 0, 1), nrow = N, ncol = xn_2) Z[, seq(1, 100, 10)] <- if_else(Z[, seq(1, 100, 10)] > 0, 1, 0) Y <- 1.0 + Z[, 1] * b1 + Z[, 2] * b2 + rnorm(N, 0, var_e) X3 <- Z[, 1:xn_1] X4 <- Z[, 1:xn_2] dat3 <- data.frame("Y" = Y, "X" = I(X3)) dat4 <- data.frame("Y" = Y, "X" = I(X4))
フィッティング
stan_glmによるフィッティング
では、これらのデータを用いてフィッティングをしてみましょう。スクリプトは以下のようになります:
n <- N D <- xn_1 p0 <- 5 # prior guess for the number of relevant variables # scale for tau (notice that stan_glm will automatically scale this by sigma) tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) # regularized horseshoe prior fit1 <- stan_glm(Y ~ X, family = gaussian(), data = dat1, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_2 p0 <- 5 tau0 <- p0/(D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit2 <- stan_glm(Y ~ X, family = gaussian(), data = dat2, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_1 p0 <- 5 tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit3 <- stan_glm(Y ~ X, family = gaussian(), data = dat3, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
D <- xn_2 p0 <- 5 tau0 <- p0 / (D-p0) * 1/sqrt(n) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit4 <- stan_glm(Y ~ X, family = gaussian(), data = dat4, prior = prior_coeff, seed = 777, chains = 4, iter = 2000)
実行画面は省略します。
結果の確認
無事にフィッティングが終わったのでまずは結果を確認しましょう。fit1オブジェクトには多くの情報が格納されていますが、以下のようにパラメータの分布を確認します(結果は一部抜粋)。
> fit1$stan_summary mean se_mean sd 2.5% 10% 25% 50% 75% 90% 97.5% n_eff Rhat (Intercept) 1.026278e+00 0.0012818960 0.08107422 0.87096060 0.92283578 9.695387e-01 1.025776e+00 1.083455e+00 1.12962235 1.18570039 4000.000 1.0002199 X1 3.908290e-01 0.0016254360 0.09798225 0.19341915 0.26638997 3.278100e-01 3.940279e-01 4.542220e-01 0.51236797 0.57793402 3633.750 0.9999048 X2 8.240328e-01 0.0013608445 0.08516982 0.65884688 0.71552972 7.672683e-01 8.238806e-01 8.816342e-01 0.93310548 0.98857084 3917.008 0.9995082 X3 -1.059357e-03 0.0005388889 0.03408233 -0.08025937 -0.03484370 -1.106505e-02 -1.177711e-04 1.032889e-02 0.03180827 0.07368474 4000.000 1.0005552 X4 -1.872770e-02 0.0007089570 0.04483838 -0.13979248 -0.07768171 -3.228712e-02 -3.977780e-03 3.213492e-03 0.01638515 0.04656703 4000.000 0.9998376 X5 2.138502e-02 0.0006738661 0.04261903 -0.03511247 -0.01201396 -1.858049e-03 6.263328e-03 3.500771e-02 0.07857940 0.13847975 4000.000 0.9993905# ︙ # 以下省略 # ︙
この結果を見るとX1とX2で概ね設定通りの値が得られているようですね。
ではここから{projpred}による変数選択に取り掛かりましょう。スクリプトは以下のようになります:
sel1 <- varsel(fit1, method = 'forward')
> sel1$varsel$vind # variables ordered as they enter during the search X2 X1 X20 X16 X19 X11 X5 X14 X18 X4 X7 X9 X8 X17 X10 X15 X13 X12 X3 X6 2 1 20 16 19 11 5 14 18 4 7 9 8 17 10 15 13 12 3 6
おおっ!ちゃんと1列目と2列目が選ばれていますね!下記のプロットを見ても、3番目以降の変数はモデルの精度に対して寄与していないことがわかると思います。なおここでelpdはexpected log predictive densityを指しますが、ちょっと情報量規準辺りの話はうかつに解説できないのでvignetteを引用するに留めておきます。
The loo method for stanreg objects provides an interface to the loo package for approximate leaveone-out cross-validation (LOO). The LOO Information Criterion (LOOIC) has the same purpose as the Akaike Information Criterion (AIC) that is used by frequentists. Both are intended to estimate the expected log predictive density (ELPD) for a new dataset.
varsel_plot(sel1, stats=c('elpd', 'rmse'))

各パラメータの分布についても見てみましょう。上位5個に選ばれた説明変数に限定してプロットしてみます。
# Visualise the three most relevant variables in the full model mcmc_areas(as.matrix(sel1), pars = names(sel1$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2))

効果のなかった変数は0を中心に集中して分布していることがわかります。
残りの各パターンについても同様に見ていきますが、個別に確認するのは面倒なので一度にまとめてしまします。
sel2 <- varsel(fit2, method = 'forward') sel3 <- varsel(fit3, method = 'forward') sel4 <- varsel(fit4, method = 'forward')
> sel2$varsel$vind X2 X1 X87 X24 X83 X71 X89 X18 X95 X85 X4 X67 X19 X16 X60 X56 X55 X53 X42 X20 2 1 87 24 83 71 89 18 95 85 4 67 19 16 60 56 55 53 42 20 > sel3$varsel$vind X2 X14 X4 X1 X18 X5 X16 X3 X9 X15 X19 X20 X6 X8 X17 X11 X7 X12 X13 X10 2 14 4 1 18 5 16 3 9 15 19 20 6 8 17 11 7 12 13 10 > sel4$varsel$vind X2 X90 X74 X45 X64 X14 X25 X52 X60 X4 X20 X16 X22 X1 X63 X41 X9 X26 X53 X5 2 90 74 45 64 14 25 52 60 4 20 16 22 1 63 41 9 26 53 5
むむ。。。
いずれのパターンでも2列目はちゃんと選ばれていますが、パターン3と4では1列目が選ばれていませんね。 プロットも見てみましょう。
varsel_plot(sel2, stats=c('elpd', 'rmse')) varsel_plot(sel3, stats=c('elpd', 'rmse')) varsel_plot(sel4, stats=c('elpd', 'rmse'))

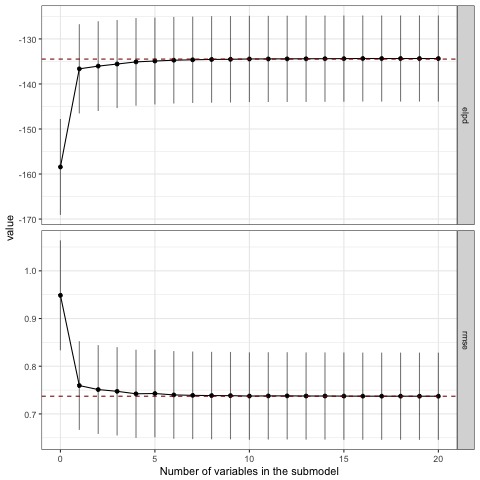
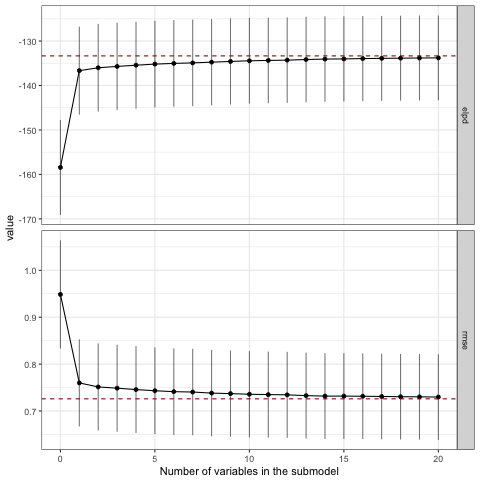
正しい変数セットが選ばれていないので当然ですが、2変数目ですでにフルモデルにおけるelpdやrmseと接するようになっており、モデルの精度改善に貢献しているのは1変数目だけという結果になっています。
パラメータの分布を見ても、パターン1と比較するといずれも分布の裾が広くなっています。さらにパターン3では正の効果を受けたためか右に裾を引く形とはなっているものの、効果のない他の変数とほとんど変わらない分布となってしまいました。ダミー変数はパラメータの推定が難しいようです。
mcmc_areas(as.matrix(sel2), pars = names(sel2$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2)) mcmc_areas(as.matrix(sel3), pars = names(sel3$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2)) mcmc_areas(as.matrix(sel4), pars = names(sel4$varsel$vind[1:5])) + coord_cartesian(xlim = c(-2, 2))



追試
では、ダミー変数が含まれる場合に真のパラメータを捉えることができる確率としてはどの程度になるのでしょうか。パターン3を100回繰り返し、そのうち何回真の変数セットを選択できるか確認してみましょう。
n <- 100 t <- 100 D <- 20 p0 <- 5 b1 <- 0.5 b2 <- 0.8 tau0 <- p0 / (D-p0) * 1/sqrt(n) out <- matrix(0, t, 2) for (i in 1:t) { x <- matrix(rnorm(n * D, 0, 1), nrow = n) x[, seq(1, D, 5)] <- ifelse(x[, seq(1, D, 5)] > 0, 1, 0) y <- 1.5 + x[, 1] * b1 + x[, 2] * b2 + rnorm(n, 0, 1) dat <- data.frame("y" = y, "x" = I(x)) prior_coeff <- hs(global_scale = tau0, slab_scale = 1) fit0 <- stan_glm(y ~ x, family = gaussian(), data = dat, prior = prior_coeff, chains = 4, iter = 2000) sel0 <- varsel(fit0) out[i, ] <- names(sel0$varsel$vind[1:2]) }
> table(out[, 1]) x2 100 > table(out[, 2]) x1 x10 x11 x12 x13 x14 x15 x17 x18 x19 x20 x3 x4 x5 x6 x7 x9 55 2 2 3 3 1 1 5 5 1 1 2 7 4 1 4 3
なんと、連続変数である2列目の選択確率は100%である一方、ダミー変数である1列目は約半数しか選択されないという結果になりました。もちろん回帰係数の大小にも影響されるのでしょうが、結構衝撃的な結果に思えます。
終わりに
これまでの実験の結果をまとめると以下のようになりそうです:
- 連続変数であれば説明変数を20から100に増やしても大きな問題なく変数を選択できそう
- ダミー変数の変数選択は難しく、今回の条件の場合、半分の確率で失敗する
- ダミー変数はパラメータの推定も難しい
実際のデータ分析の現場では真のパラメータを予め知ることができないため、変数選択の結果を受け入れざるを得ないことがあるかと思います。しかし今回の実験の結果からは「真の変数セットを選択できる確率は半分程度しかない」ことが示されており、機械的な変数の取捨選択がどれほど危険であるかを教えてくれているのではないでしょうか。
とは言え今回実験に使用した{projpred}は便利なlibraryであると思いますので、これから活用しつつも引き続き変数選択の方法について探していこうと思います。