glmnetをもう少し理解したい③
前回の記事では R の関数 elnet の中で elnet という Fortran のサブルーチンが呼ばれ(やっぱりややこしいですね)、さらに type.gaussian の値( covariance と naive )によって elnetu と elnetn のいずれかが呼ばれるところまで確認しました。
今回は elnetu の中身を見ていきます。
過去の記事はこちらです。
elnetu の実装
それでは早速 elnetu を見ていきましょう。 elnetu は elnet と同様にそれほど大きくないのでいきなり内容の確認に入りますが、処理としては以下の手順になっているようです:
- 前処理
- 標準化
- フィッティング
- 後処理
まずは前処理ですが、メモリの割り付けのあとに chkvars というサブルーチンを呼び出しています。
subroutine elnetu(parm,no,ni,x,y,w,jd,vp,cl,ne,nx,nlam, flmin,ulam,thr,isd,intr,maxit, lmu,a0,ca,ia,nin,rsq,alm,nlp,jerr) implicit double precision(a-h,o-z) double precision x(no,ni),y(no),w(no),vp(ni),ulam(nlam),cl(2,ni) double precision ca(nx,nlam),a0(nlam),rsq(nlam),alm(nlam) integer jd(*),ia(nx),nin(nlam) double precision, dimension (:), allocatable :: xm,xs,g,xv,vlam integer, dimension (:), allocatable :: ju allocate(g(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xm(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xs(1:ni),stat=jerr) if(jerr.ne.0) return allocate(ju(1:ni),stat=jerr) if(jerr.ne.0) return allocate(xv(1:ni),stat=jerr) if(jerr.ne.0) return allocate(vlam(1:nlam),stat=jerr) if(jerr.ne.0) return ! 1. 前処理 call chkvars(no,ni,x,ju) if(jd(1).gt.0) ju(jd(2:(jd(1)+1)))=0 if(maxval(ju) .gt. 0)goto 10071 jerr=7777 return 10071 continue
この chkvars では x の各変数について一行目の値と異なる値が二行目以降にあるかを確認し、 ju に格納しています。
subroutine chkvars(no,ni,x,ju) implicit double precision(a-h,o-z) double precision x(no,ni) integer ju(ni) ! ここから各変数のチェックを開始 do 11061 j=1,ni ju(j)=0 t=x(1,j) ! 1行目の値を取得 ! ここから2行目の値を確認する do 11071 i=2,no ! t は x(1, j) なので、各変数 j について 1 行目の値と等しいかを確認している if(x(i,j).eq.t) goto 11071 ! 等しければ次の行へ ju(j)=1 ! 等しくない数値があれば ju を 1 にして次の変数へ goto 11072 11071 continue 11072 continue 11061 continue continue return end
異なる値がなければ全ての値は同じということになりますので、例えば回帰係数を推定する意味はありません。
後続の処理ではこの ju を参照してスキップするかを決めている箇所が多々出てきます。
続いて standard というサブルーチンを呼び出して標準化を行います。
! 2. 標準化 call standard(no,ni,x,y,w,isd,intr,ju,g,xm,xs,ym,ys,xv,jerr)
この standard とうサブルーチンは結構大きく見えますが、切片の有無で処理を分けているため重複部分があります。
処理の内容としては:
- 重みの変換
- y と x の更新
- y と x の内積(共分散)を計算
となっています。
まずは重みの変換を確認してみると、重み w を「重みの総和あたりの重み」に変換し、
さらにその平方根をとったものを v として定義しています。
またその次から、先に述べたように切片の有無によって処理を分けています。
subroutine standard(no,ni,x,y,w,isd,intr,ju,g,xm,xs,ym,ys,xv,jerr) implicit double precision(a-h,o-z) double precision x(no,ni),y(no),w(no),g(ni),xm(ni),xs(ni),xv(ni) integer ju(ni) double precision, dimension (:), allocatable :: v allocate(v(1:no),stat=jerr) if(jerr.ne.0) return ! 1. 重みの変換 w=w/sum(w) v=sqrt(w) ! intr は intercept なので切片が 0 であるかで判定 ! 切片が 0 でない場合は 10141 に飛ばされる if(intr .ne. 0) goto 10141
以降の処理ではこの v を y や x に対して掛け合わせるのですが、全ての観測値の重みが等しい単純なパターンを想定すると w には $1/n$ 、v にはその平方根が入ります。
例えば観測値の数が 100 であれば $w = 1/100 = 0.01$ 、$v = sqrt(1/100) = 0.1$ となります。
ではこのような w や v を使って何をやっているかというと、 y に対しては:
ということをしています。
! 2. y と x の更新 ! 以下のセクションでは y と x それぞれについて観測値の重みを使って色々と調整する ! まずは y ym = 0.0 y = v*y ys = sqrt(dot_product(y,y)-dot_product(v,y)**2) y = y/ys
ただこの説明だけでは意味が分からないと思いますので少し式を整理してみましょう。
もとの y および w を $y0$ 、 $w0$ とおくと、
となります。
また ys の二乗(平方根を取る前) $ (ys)^{2} $ は:
と書けます。
ここで $w$ は観測値に対する重み $w0$ をその総和で除した形(単純なパターンでは $\frac{1}{n}$ )となっていることを思い出すと、これを乗じたものの総和は重み付き平均となります。
そうすると右辺の第一項はもともとの y ($y0$)の二乗の重み付き平均、第二項は重み付き平均の二乗が得られていることがわかります。
二乗の平均から平均の二乗を引いたものと言えば分散ですので、その平方根をとった ys は $y0$ の重み付き標準偏差を得ているようです
(ところで $w$、$w0$ は添字 $i$ を付けるべきですが、はてなブログの LaTeX がなぜか崩れるので省略しています)。
実際にサンプルデータで計算してみましょう。 まずは以下のような簡単なデータで二乗の平均から平均の二乗を引いたものが分散になることを確認します。
# 適当なデータ a <- c(5, 5, 6, 7, 9) # 一般的な分散の計算 mean((a - mean(a))^2) # 二乗の平均から平均の二乗を引いてみる mean(a^2) - mean(a)^2 # R の var を使う var(a) * 4 / 5
[1] 2.24 [1] 2.24 [1] 2.24
上の例ではいずれも同じ値を返していることがわかります。
なお var を使った計算では不偏分散ではなく標本分散に修正しました。
続いて先の計算にしたがった場合に、やはり同じように分散・標準偏差が得られるかを見てみます。
set.seed(123) n <- 10 y0 <- rnorm(n) w0 <- rep(1, n) w <- w0/sum(w0) v <- sqrt(w) y <- v*y0 ys <- sqrt(y %*% y - (v %*% y)^2) y_new <- y/ys[1]
> mean((y0 - mean(y0))^2) # 一般的な分散の計算 [1] 0.8187336 > mean(y0^2) - mean(y0)^2 # 二乗の平均から平均の二乗を引く [1] 0.8187336 > var(y0) * (n-1) / n # R の var を使って [1] 0.8187336 > (ys^2)[1] # 計算した値 [1] 0.8187336
$(ys)^{2}$ が $y0$ の分散になっていることが確認できますね。
ということで、先ほどの処理では w や v を使ってもともとの y の重み付き標準偏差を計算し、その値で重み付きの y を除していることがわかりました。
このサブルーチンの名前が standard なので当然ですが、標準化をしているようです。
x についても基本的に同様の処理を行っており、v を使って重み付き標準偏差を計算・標準化をしています。
ただし最後に重み付き平均の二乗 / 分散 に 1 を加算したものを xv に格納しており、これを x の分散としているようなのですが、これが良くわかりませんでした。
ちなみに ju は先ほど説明したように各変数に異なる数値・バラつきがあるかを示すもので、バラつきがなければさっさとループを抜けて次の変数に移っていることがわかります。
! x do 10151 j=1,ni ! ni は nvars if(ju(j).eq.0)goto 10151 xm(j) = 0.0 x(:,j) = v*x(:,j) ! x にも重みを乗じる xv(j) = dot_product(x(:,j),x(:,j)) ! x の二乗の重み付き平均 ! isd は標準化するかの指定で、標準化する場合は 1 が入っており 10171 に飛ばされない if(isd .eq. 0) goto 10171 xbq = dot_product(v, x(:,j))**2 ! x の重み付き平均の二乗 vc = xv(j)-xbq ! 重み付き分散 xs(j) = sqrt(vc) ! 重み付き標準偏差。 ys と対応している。 x(:,j) = x(:,j)/xs(j) ! 標準偏差で割って標準化。 y/ys と対応している。 ! これはよくわからない xv(j) = 1.0 + xbq/vc ! 重み付き平均の二乗 / 分散 に 1 を加算 goto 10181 10171 continue xs(j)=1.0 10181 continue continue 10151 continue continue goto 10191
切片が 0 でない場合はこちらにきます(基本はこっち)が、処理は上記と大体同じです。
y、x ともに値を更新する前に重み付き平均を引いているところが違う点ですね。
! 切片が 0 でない場合ここに来る ! 基本はこっち 10141 continue ! x do 10201 j=1,ni if(ju(j).eq.0)goto 10201 xm(j) = dot_product(w,x(:,j)) ! x の重み付き平均 x(:,j) = v*(x(:,j)-xm(j)) ! 重み付き平均を引いてから重みを乗じる xv(j) = dot_product(x(:,j),x(:,j)) ! 二乗の重み付き平均 if(isd.gt.0) xs(j) = sqrt(xv(j)) ! 重み付き標準偏差 10201 continue continue if(isd .ne. 0)goto 10221 xs = 1.0 goto 10231 10221 continue do 10241 j=1,ni if(ju(j).eq.0)goto 10241 x(:,j) = x(:,j)/xs(j) ! 標準化はここで実行 10241 continue continue xv=1.0 10231 continue continue ym = dot_product(w,y) ! y の重み付き平均 y = v*(y-ym) ! y から重み付き平均を引いたものに重みを乗じる ys = sqrt(dot_product(y,y)) ! 二乗和(分散)の平方根(SD) y = y/ys ! 標準化
次の処理は共通のもので、y と x の内積を計算し、 g に格納します。
単純に y と x の内積を計算しているように見えますが、ここでの y は
、x は
となっているので、その内積は重み付き共分散をそれぞれの標準偏差の積で除したもの、つまり重み付きの相関係数となっているはずです。
! 3. 内積(重み付き相関係数)を格納 10191 continue continue g = 0.0 do 10251 j=1,ni ! j 番目の変数にバラツキがあるなら g に y と x の内積(共分散)を格納する ! ただしこの時点での y と x はそれぞれ標準偏差で除したものとなっている if(ju(j).ne.0) g(j) = dot_product(y, x(:,j)) 10251 continue continue deallocate(v) return end
先のサンプルデータで確かめてみましょう。
重みが全て等しいという単純なパターンでは、更新された y と x の内積が相関係数になっていることが確認できます。
set.seed(123) n <- 10 y0 <- rnorm(n) x0 <- rnorm(n) w0 <- rep(1, n) w <- w0/sum(w0) v <- sqrt(w) y <- v*(y0 - (w %*% y0)[1]) ys <- sqrt(y %*% y) y_new <- y/ys[1] x <- v*(x0 - (w %*% x0)[1]) xs <- sqrt(x %*% x) x_new <- x/xs[1]
> (y_new %*% x_new)[1] # 内積 [1] 0.5776151 > cor(y_new, x_new) # 更新後の y と xの相関係数 [1] 0.5776151 > cor(y0, x0) # 元の値の相関係数 [1] 0.5776151
一方重みが観測値によって異なる場合はというと、これは近い値になるものの完全に一致はしませんでした(でもこれなんでだろう、一致するような気がするんだけど)。
set.seed(123) n <- 10 y0 <- rnorm(n) x0 <- rnorm(n) w0 <- rep(1, n) - 0.5 * ifelse(runif(n) > 0.8, 1, 0) # 一部のデータに対して重みを小さくしている w <- w0/sum(w0) v <- sqrt(w) y <- v*(y0 - (w %*% y0)[1]) ys <- sqrt(y %*% y) y_new <- y/ys[1] x <- v*(x0 - (w %*% x0)[1]) xs <- sqrt(x %*% x) x_new <- x/xs[1]
> (y_new %*% x_new)[1] [1] 0.5687947 > cor(y_new, x_new) [1] 0.5687133 > cor(y0, x0) [1] 0.5776151
ところで重み調整後の y と x の内積が相関係数と近似(一致?)するなら、個別のデータのペアが相関に対してどのような影響を持っているかを評価できるのではないでしょうか。
内積ではなく各ペアの掛け算語の値を見てみると、6 番目と 8 番目の値が高い値を示していることがわかります。
このデータの重み付き相関係数は 0.568 ぐらいだったので、この 2 つの観測値の影響が大きそうです。
> cbind(1:n, y_new * x_new) [,1] [,2] [1,] 1 -0.0744142551 [2,] 2 -0.0043928887 [3,] 3 0.0261049036 [4,] 4 0.0004833048 [5,] 5 -0.0025033504 [6,] 6 0.2852904868 [7,] 7 0.0104270429 [8,] 8 0.3466035906 [9,] 9 -0.0413263433 [10,] 10 0.0225221645
実際にデータを見てみると、 6 番と 8 番のデータは他の観測値と比べて関連性が強そうに見えます。
> cbind(y_new, x_new) y_new x_new [1,] -0.233569767 0.31859541 [2,] -0.117117800 0.03750829 [3,] 0.513582873 0.05082900 [4,] -0.011106121 -0.04351698 [5,] 0.009617489 -0.26029149 [6,] 0.568708951 0.50164585 [7,] 0.126538479 0.08240215 [8,] -0.481982832 -0.71912020 [9,] -0.278126098 0.14858851 [10,] -0.136535493 -0.16495465
6 と 8 番目のデータを塗り分けてみるとわかりやすいですね。
cols <- c(1, 1, 1, 1, 1, 3, 1, 3, 1, 1) + 1 plot(y ~ x, col = cols, pch = 16)
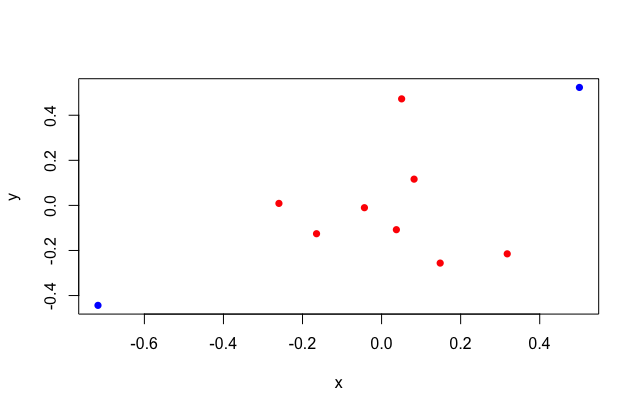
以上で y と x について標準化が終わったのでstandard から elnet に帰ってくると今度は回帰係数の上限・下限についても標準化を行います。
また flmin が 1 以上の場合は vlam を更新するのですが、 flmin は lambda が指定された場合に 1 が入り、そうでなければ $[0, 1)$ の実数が期待されるパラメータでした。
なので lambba が指定された場合(= flmin が 1 のとき)に vlam が y の重み付き標準偏差で調整される事になります。
この vlam は後続の処理(フィッティング)では ulam として渡されるものですが、ulam は lambda の指定がなければ 1 、指定があればその降順となるものでした。
要するに lambda の大きさについても標準化するよ、という事のようですね。
! jerr に 0 でない値が入っていると return if(jerr.ne.0) return ! cl は glmnet で cl = rbind(lower.limits, upper.limits) と定義される ! 回帰係数の上限・加減 cl=cl/ys ! 標準化の指定が 0 であれば以下はスキップ if(isd .le. 0) goto 10091 ! 説明変数ごとに標準偏差を乗じる do 10101 j=1,ni cl(:,j)=cl(:,j)*xs(j) 10101 continue continue 10091 continue ! flmin は glmnet のなかで flmin = as.double(lambda.min.ratio) で定義される ! ここで lambda.min.ratio = ifelse(nobs < nvars, 0.01, 1e-04) if(flmin.ge.1.0) vlam=ulam/ys
ではフィッティングです。
ここで呼ばれる elnet1 こそが {glmnet} の本体となり、回帰係数の計算はここで行われます。
この中ではもうサブルーチンはほとんど呼ばれず、初期パラメータを取ってくるものとプログレスバーを表示するためのものだけです。
ようやくたどり着きました、今回も長かったですね。
! 3. フィッティング ! 本体である elnet1 の呼び出し call elnet1(parm,ni,ju,vp,cl,g,no,ne,nx,x,nlam,flmin,vlam,thr,maxi,xv, lmu,ca,ia,nin,rsq,alm,nlp,jerr)
このサブルーチンは量はそこそこ(180行程度)なのですが、ループが込み入っていて紹介が長くなるので今回はここまでです。 また次回。