GAMをもう少し理解したい④
前回の続きです。過去記事はこちらから。
GAMの実装
bakfit
さて bakfit ですが、このサブルーチンはバックフィッティングというアルゴリズムを定義しています。このアルゴリズムは、簡単に言えば「関心のある平滑化対象変数を順番に残差に対してフィッティングしていく」方法です。Wikipediaのバックフィッティングのページからアルゴリズムの部分について抜粋しましょう:
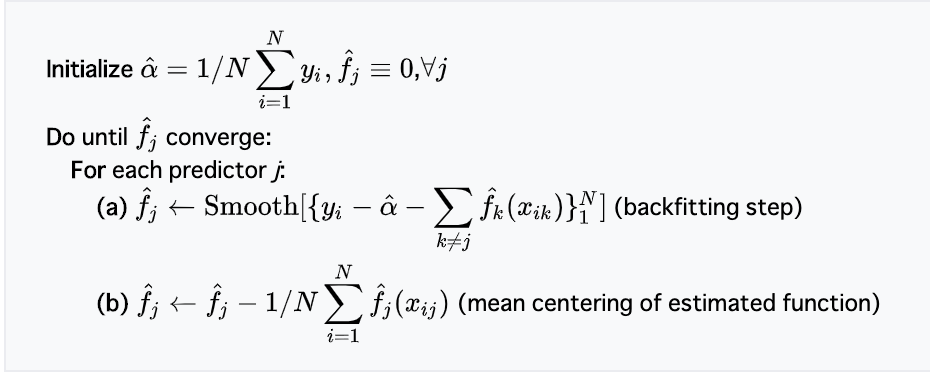
ポイントは4行目の (a) のところで、
とあるように、目的変数から定数部(線形部分)および関心のある平滑化対象変数"以外"(非線形部分)を引いています。すなわち「平滑化対象変数で説明される部分」と「確率的な誤差」で構成される部分のみを残し、平滑化を行なっていることがわかります。これを非線形としたい変数全てについて収束するまで順次繰り返す、というのがバックフィッティングの流れです。
ちなみにこのバックフィッティング、Wikipediaのページでは以下のような説明があります:
the backfitting algorithm is equivalent to the Gauss–Seidel method algorithm for solving a certain linear system of equations.
さらにGauss–Seidel法について調べると(こちら)、これはn元の連立一次方程式を反復的に解くための手法であることが解説されているのですが、その中で以下の記述があります:
The Gauss–Seidel method now solves the left hand side of this expression for x, using previous value for x on the right hand side.
で、これは以下のように解くことができます:
ここで括弧の中に着目すると、$b$から$ax$が順次引かれている(二項目と三項目)のですが、総和記号のインデックスには$i$が含まれていません。つまり更新の対象である$i$番目の$x$以外を順番に引いており、バックフィッティングと同じような計算になっていることがわかります。なお括弧の中の三項目は添え字が (k) ですが、二項目では (k+1) になっており、更新後の$x$を直接使っていることがわかります。さらにちなみに、ここで逐次更新するのではなく一度全ての解を求めてから一斉に更新する方法をヤコビ法といいます。
では上記のアルゴリズムが bakfit でどのように実装されているのかを確認してみましょう。と言いつつ実は bakfit 自体は基本的に以下のように backf1 を呼び出しているだけです。
subroutine bakfit(x,npetc,y,w,which,spar,dof,match,nef, etal,s,eta,beta,var,tol, qr,qraux,qpivot,effect,work) implicit double precision(a-h,o-z) logical ifvar integer npetc(7),iter integer n,p,q,which(*),match(*),nef(*),nit,maxit,qrank,qpivot(*) double precision x(*),y(*),w(*),spar(*),dof(*), etal(*),s(*),eta(*),beta(*),var(*),tol, qr(*),qraux(*),effect(*),work(*) n=npetc(1) p=npetc(2) q=npetc(3) ifvar=.false. if(npetc(4)==1)ifvar=.true. maxit=npetc(6) qrank=npetc(7) do i=1,q{work(i)=dof(i)} ### ここで backf1 を呼び出している call backf1(x,n,p,y,w,q,which,spar,dof,match,nef, etal,s,eta,beta,var,ifvar,tol,nit,maxit, qr,qraux,qrank,qpivot,effect,work(q+1),work(q+n+1), work(q+2*n+1),work(q+3*n+1),work(q+4*n+1)) npetc(7)=qrank return end
なので backf1 を確認することにしましょう。
backf1
前回同様まずは backf1 の処理全体をさっと眺めて見通しを良くします。 backf1 ではざっくりと
- 前処理
- バックフィッティング
etaを再定義
という処理が行われます。
subroutine backf1(x,n,p,y,w,q,which,spar,dof,match,nef, etal,s,eta,beta,var,ifvar,tol,nit,maxit, qr,qraux,qrank,qpivot,effect,z,old,sqwt,sqwti,work) implicit double precision(a-h,o-z) logical ifvar integer n,p,q,which(q),match(n,q),nef(q),nit,maxit,qrank,qpivot(p) double precision x(n,p),y(n),w(n),spar(q),dof(q), etal(n),s(n,q),eta(n),beta(p),var(n,q),tol, qr(n,p),qraux(p),effect(n),work(*) double precision z(*),old(*),dwrss,ratio double precision sqwt(n),sqwti(n) logical anyzwt double precision deltaf, normf,onedm7 integer job,info onedm7=1d-7 job=1101;info=1 if(q==0)maxit=1 ratio=1d0 ## 1. 前処理 ### データに重みをつける anyzwt=.false. do i=1,n{ if(w(i)>0d0){ sqwt(i)=dsqrt(w(i)) sqwti(i)=1d0/sqwt(i) } else{ sqwt(i)=0d0 sqwti(i)=0d0 anyzwt=.true. } } ### QR分解する if(qrank==0){ do i=1,n{ do j=1,p{ qr(i,j)=x(i,j)*sqwt(i) } } do j=1,p{qpivot(j)=j} call dqrdca(qr,n,n,p,qraux,qpivot,work,qrank,onedm7) } ### eta に 非線形項 s(i,j) を加算する do i=1,n{ eta(i)=0d0 for(j=1;j<=q;j=j+1){ eta(i)=eta(i)+s(i,j) } } ## 2. バックフィッティング nit=0 while ((ratio > tol )&(nit < maxit)){ deltaf=0d0 nit=nit+1 ### まずは Linear part + error 部分に最小二乗法を当てはめる do i=1,n{ z(i)=(y(i)-eta(i))*sqwt(i) old(i)=etal(i) } call dqrsl(qr,n,n,qrank,qraux,z,work(1),effect(1),beta, work(1),etal,job,info) ### 重みの逆数で戻し、 etal を更新 do i=1,n{ etal(i)=etal(i)*sqwti(i) } ### 次に平滑化対象の変数についてループ for(k=1;k<=q;k=k+1){ j=which(k) do i=1,n{ old(i)=s(i,k) z(i)=y(i)-etal(i)-eta(i)+old(i) } if(nit>1){dof(k)=0d0} ### splsmで平滑化 call splsm(x(1,j),z,w,n,match(1,k),nef(k),spar(k), dof(k),s(1,k),s0,var(1,k),ifvar,work) do i=1,n{ eta(i)=eta(i)+s(i,k)-old(i) etal(i)=etal(i)+s0 } deltaf=deltaf+dwrss(n,old,s(1,k),w) } ### whileループの打ち切り判定 normf=0d0 do i=1,n{ normf=normf+w(i)*eta(i)*eta(i) } if(normf>0d0){ ratio=dsqrt(deltaf/normf) } else {ratio = 0d0} } ### 3. eta を再定義 do j=1,p {work(j)=beta(j)} do j=1,p {beta(qpivot(j))=work(j)} if(anyzwt){ do i=1,n { if(w(i) <= 0d0){ etal(i)=0d0 do j=1,p{ etal(i)=etal(i)+beta(j)*x(i,j) } } } } do i=1,n eta(i)=eta(i)+etal(i) do j=1,q { call unpck(n,nef(j),match(1,j),var(1,j),old) do i=1,n {var(i,j)=old(i)} } return end
3つ目の工程で eta の再定義とあるのですが、これまでの処理(〜 s.wam)において eta は「 y をリンク関数で変換したもの」として扱われてきました。一方 backf1 の中では 「平滑化対象変数によって構成される部分」(非線形/平滑化部分)として扱われており、混乱しやすいので注意が必要です。つまり backf1 の中では y を「線形部分」と「非線形(平滑化)部分」に分割し、前者を etal 、後者を eta として計算が行われます。
では一つずつ見ていきましょう。
1. 前処理
まずは前処理です。ここでは
という処理が行われます。
### weight の平方根をとって逆数にする anyzwt=.false. do i=1,n{ if(w(i)>0d0){ sqwt(i)=dsqrt(w(i)) ## Fortranの組み込み関数。sqrt() sqwti(i)=1d0/sqwt(i) ## weight の逆数 } else{ sqwt(i)=0d0 sqwti(i)=0d0 anyzwt=.true. } } ### qrank が 0 のときは、x に重みを加えた上で QR 分解する if(qrank==0){ do i=1,n{ do j=1,p{ ### 重みを乗じた x を生成 qr(i,j)=x(i,j)*sqwt(i) # qr は n*p の行列 } } do j=1,p{qpivot(j)=j} ### qvivot は長さ p の integer。1~p の数字を格納 ### QR分解。dqrdca のソースは以下 ### https://github.com/cran/gam/blob/master/inst/ratfor/linear.r call dqrdca(qr,n,n,p,qraux,qpivot,work,qrank,onedm7) } ### eta に 非線形項 s(i,j) を加算する ### ただしここで eta は fitted value ではなく 0 スタート ### s は線形部分とは独立な平滑化部分で、バックフィッティングで更新する do i=1,n{ eta(i)=0d0 # 0.0 にリセット for(j=1;j<=q;j=j+1){ # 平滑化対象の変数について eta(i)=eta(i)+s(i,j) # 平滑化部分を順次加算していく } }
上のブロックでQR分解を行なっていますが、これは次の工程で線形部分に対して通常の回帰を実行するためです。以前の記事で glm がどのように実装されているかを調べた際、 glm では、
dqrdc2というサブルーチンを用いてQR分解dqrslというサブルーチンで最小二乗法を当てはめ
という処理で解が得られることを示しましたが、 glm 同様に gam においても線形部分のフィッティングではQR分解によって最小二乗解を求める、という流れになっているようです。
2. バックフィッティング
では続いてバックフィッティングの実装を見ていきましょう。ここが、ある意味で gam の本体とも言えるルーチンになります。
### while ループ開始 nit=0 while ((ratio > tol )&(nit < maxit)){ # ratio のデフォルトは 1.0 。 tol は多分 0.0005 # first the linear fit deltaf=0d0 nit=nit+1 # イテレータに +1 ### まずは Linear part + error 部分に最小二乗法を当てはめる ### y から非線形項を減じたもの(Linear part + error)に重みを乗じて z を更新(これを y として dqrsl に渡す) # etal を old に格納。ループ1回目の時点では etal は Null? do i=1,n{ z(i)=(y(i)-eta(i))*sqwt(i) old(i)=etal(i) } ### https://github.com/wch/r-source/blob/trunk/src/appl/dqrsl.f ### dqrsl の6個目の引数として z を渡しているが、これは y になる ### etal は11番目の引数として渡しているが、これは xb 。 call dqrsl(qr,n,n,qrank,qraux,z,work(1),effect(1),beta, work(1),etal,job,info) ### 重みの逆数で戻し、 etal を更新 ### etal は y の予測値の線形部分 do i=1,n{ etal(i)=etal(i)*sqwti(i) }
まずは上のブロックで線形部分のフィッティングが行われます。 dqrsl の直前の処理に注目すると、 y から eta を減じたものを z として定義し、これを dqrsl の引数として渡しています。すなわち目的変数から eta (非線形部分)を減じた、線形部分ですね。これを、先ほど解説したように dqrsl というサブルーチンに渡し、最小二乗法による解を得ます。引数には eta ではなく etal が入っていることに注意しましょう。この etal は直後の処理で重みを乗じた上で後続の処理に引き渡されます。
続いて平滑化対象変数の処理に入ります。
### ここで平滑化対象の変数についてループ for(k=1;k<=q;k=k+1){ # 平滑化対象の変数ごとに j=which(k) do i=1,n{ ### old に k 番目の平滑化対象変数の値を入れる old(i)=s(i,k) ### y から etal (Linear part)と eta (Nonlinear part) を引き、old (k 番目の Nonlinear part) を足している ### 残差 + k 番目の平滑化変数の値になっている z(i)=y(i)-etal(i)-eta(i)+old(i) } ### df は 0 にリセットされてしまう if(nit>1){dof(k)=0d0} ### splsm を呼びだす ### 切片と k 番目の平滑化変数を x として渡す ### 9番目の引数 s が splsm 内での平滑化変数 smo なので s が更新される call splsm(x(1,j),z,w,n,match(1,k),nef(k),spar(k), dof(k),s(1,k),s0,var(1,k),ifvar,work) do i=1,n{ ### eta を更新 ### 古い eta にk番目の非線形部分を加算して、古い非線形部分を減じる) eta(i)=eta(i)+s(i,k)-old(i) ### etal を更新(古い etal に s0 を乗じる。) ### s0 は weighted mean of y etal(i)=etal(i)+s0 } ### deltaf を更新(while ループの打ち切り判定) deltaf=deltaf+dwrss(n,old,s(1,k),w) } # ここまで for ループ
細かな処理はコメントとして書いてありますが、このブロックでは平滑化の対象となる変数について平滑化を実行して s を更新します。ポイントは
z(i)=y(i)-etal(i)-eta(i)+old(i)
のところで、この記事の冒頭でバックフィッティングのアルゴリズムを解説した際に「関心のある平滑化対象変数を順番に残差に対してフィッティングしていく」と述べましたが、そのために残差を求めているのが上の式になります。 etal は線形部分、 eta は非線形部分なので両者を引くと確率的な誤差しか残りませんが、そこに old(i) つまり s(i, k) を加算することで、k番目の平滑化対象変数 + 確率的な誤差のみが残ります。
続いてこの誤差に対して平滑化を行なっているのが
splsm(x(1,j),z,w,n,match(1,k),nef(k),spar(k), dof(k),s(1,k),s0,var(1,k),ifvar,work)
の部分です。この splsm は内部でさらに sbart というCのサブルーチンを呼び出しているのですが、この解説を始めるとキリがないのでまた別の機会に取っておきましょう。
平滑化により s が更新されたら、 eta にもk番目の平滑化対象変数の更新を反映させ、最後に while ループの打ち切り判定のための指標を計算します。
### normf の更新(while ループの打ち切り判定) normf=0d0 do i=1,n{ normf=normf+w(i)*eta(i)*eta(i) } ### ratio(while ループの判定に使われる)を計算 if(normf>0d0){ ratio=dsqrt(deltaf/normf) } else {ratio = 0d0} # call DBLEPR("ratio",-1,ratio,1) }
3. eta の再定義
以上の工程で十分に収束したと判断されたらバックフィッティングアルゴリズムは終了し、 s.wam に値を返す処理に入ります。冒頭で解説したように backf1 内では eta は非線形部分として扱われていたので、これを線形部分と加算して元の eta に戻します。なお beta は線形部分の各変数の回帰係数です。
### etal を再定義 do j=1,p {work(j)=beta(j)} do j=1,p {beta(qpivot(j))=work(j)} if(anyzwt){ do i=1,n { if(w(i) <= 0d0){ etal(i)=0d0 do j=1,p{ etal(i)=etal(i)+beta(j)*x(i,j) } } } } ### 非線形項 + 線形項として eta を再定義 do i=1,n eta(i)=eta(i)+etal(i) ### 結果をまとめる do j=1,q { call unpck(n,nef(j),match(1,j),var(1,j),old) do i=1,n {var(i,j)=old(i)} } return end
さて、これで backf1 および bakfit の処理は終了したので s.wam に戻ることになります。 s.wam の残りの工程では、前回記事で確認したように結果を格納したオブジェクトである rl を生成するのでした。それと元々のデータを順位で置き換える形で生成された smooth.frame をまとめて返します。
さらに s.wam を抜けると gam.fit 内でのループに戻ってくるわけですが、これは前々回記事で解説した通り、残差からデビアンスを計算した上でループの打ち切りを判定します。
gam.fit
収束が十分であれば、 gam.fit のループを抜けます。残りの工程は基本的に結果をまとめあげて gam に返すだけのようです。
### gam.fit に戻ってきた fitqr <- fit$qr xxnames <- xnames[fitqr$pivot] nr <- min(sum(good), nvars) if (nr < nvars) { Rmat <- diag(nvars) Rmat[1:nr, 1:nvars] <- fitqr$qr[1:nr, 1:nvars] } else Rmat <- fitqr$qr[1:nvars, 1:nvars] Rmat <- as.matrix(Rmat) Rmat[row(Rmat) > col(Rmat)] <- 0 dimnames(Rmat) <- list(xxnames, xxnames) names(fit$residuals) <- ynames names(mu) <- ynames names(eta) <- ynames ### eta and mu fit$additive.predictors <- eta fit$fitted.values <- mu names(fit$weights) <- ynames names(fit$effects) <- c(xxnames[seq(len = fitqr$rank)], rep.int("", sum(good) - fitqr$rank)) if (length(fit$smooth) > 0) fit$smooth.frame <- smooth.frame[smooth.labels] wtdmu <- if (a$intercept) sum(weights * y)/sum(weights) else linkinv(offset) nulldev <- sum(dev.resids(y, wtdmu, weights)) n.ok <- nobs - sum(weights == 0) nulldf <- n.ok - as.integer(a$intercept) rank <- n.ok - fit$df.residual aic.model <- aic(y, nobs, mu, weights, new.dev) + 2 * rank if (!is.null(fit$smooth)) { nonzeroWt <- (wz > 0) nl.chisq <- gam.nlchisq(fit$qr, fit$residuals, wz, fit$smooth) } else nl.chisq <- NULL fit <- c(fit, list(R = Rmat, rank = fitqr$rank, family = family, deviance = new.dev, aic = aic.model, null.deviance = nulldev, iter = iter, prior.weights = weights, y = y, df.null = nulldf, nl.chisq = nl.chisq)) fit }
gam
ようやく gam に帰ってきました。 gam.fit を呼び出した以降の処理は以下のブロックだけです。特定の条件下においてNull Deviance(切片のみ考慮されたモデルによる逸脱度)を計算し、結果をまとめあげて返します。
### offset が指定されており intercept 項がある場合 if (length(offset) && attr(mt, "intercept") > 0) { fit$null.dev <- glm.fit(x = X[, "(Intercept)", drop = FALSE], y = Y, weights = weights, offset = offset, family = family, control = control[c("epsilon", "maxit", "trace")], intercept = TRUE)$deviance } if (model) fit$model <- mf fit$na.action <- attr(mf, "na.action") if (x) fit$x <- X if (!y) fit$y <- NULL fit <- c(fit, list(call = call, formula = formula, terms = mt, data = data, offset = offset, control = control, method = method, contrasts = attr(X, "contrasts"), xlevels = .getXlevels(mt, mf))) class(fit) <- c("Gam", "glm", "lm") if (!is.null(fit$df.residual) && !(fit$df.residual > 0)) warning("Residual degrees of freedom are negative or zero. This occurs when the sum of the parametric and nonparametric degrees of freedom exceeds the number of observations. The model is probably too complex for the amount of data available.") fit }
終わりに
以上で終わりです!長くなりましたが、ようやく gam の内部で何が行われているかを確認することができました。振り返ると、 gam という関数のコアとなる部分では:
- バックフィッティングによる非線形項のフィッティング(
bakfitおよびbackf1) - バックフィッティングに渡すためにデータを順位に置き換える(
s.wam) {general, s, lo}.wamのいずれのエンジンに渡すかを特定し、bf.callを作成(gam.fit)gam.fitに渡すための諸々の設定(gam)
といった処理が行われているようでした。またバックフィッティングというアルゴリズムは、端的には「関心のある変数による影響のみを残してフィッティングすることを繰り返す」というものであることがわかりました。
一方で、今回の一連の記事では平滑化の仕組みを追いかけることがまだ出来ていません。また平滑化の関数にしても s.wam しか見ておらず、 lo.wam や general.wam の挙動を確認していません。その辺りもいずれ調べたいですね。